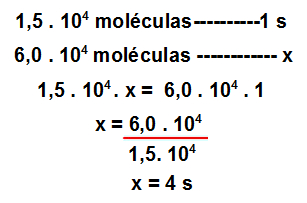Questão 1
Um reservatório de uma empresa especializada em gases contém o gás hidrogênio a uma pressão P e uma temperatura T. Sabe-se que esse reservatório apresenta uma perda por difusão de 6,0 . 104 moléculas por segundo. Quando comparado a outro reservatório da empresa contendo o gás oxigênio, nas mesmas condições de pressão e temperatura, podemos dizer que ele perderá o mesmo número de moléculas em qual tempo? (Dados: H = 1 g/mol; O = 16 g/mol)
a) 10 s
b) 4 s
c) 6 s
d) 2 s
e) 8 s
Questão 2
A velocidade de efusão do gás hélio é igual a 6,75 km/min, em determinadas condições de pressão e temperatura. Nas mesmas condições, qual será a velocidade de efusão do gás oxigênio em km/h? (Dados: He = 2 g/mol; O = 16 g/mol)
a) 1,7865 km/h
b) 1,6875 km/h
c) 101,25 km/h
d) 102,15 km/h
e) 7,65 km/h
Questão 3
(Mackenzie-SP) Dois recipientes separados, iguais, contendo, respectivamente, moléculas de hélio e dióxido de enxofre, nas mesmas condições de pressão e temperatura, possuem orifício por onde os gases escapam. Se a velocidade de efusão do hélio é de 6,0 . 103 km/h, então, a velocidade de efusão: (Dados: He=4; S=32; O=16).
a) do dióxido de enxofre é quatro vezes maior que a do hélio.
b) do hélio é oito vezes maior que a do dióxido de enxofre.
c) dos dois gases é igual.
d) do dióxido de enxofre é 1,5 . 103 km/h.
e) do hélio é dezesseis vezes menor que a do dióxido de enxofre.
Questão 4
(F.C. Chagas-BA) Metano começa a escapar por um pequeno orifício com a velocidade de 36 mililitros por minuto. Se o mesmo recipiente, nas mesmas condições, contivesse brometo de hidrogênio, qual seria a velocidade inicial de escape pelo mesmo orifício?
Dados: H=1; C=12; Br=80.
a) (4 . 36)/9 mililitros por minuto
b) (16 . 36)/81 mililitros por minuto
c) 9 / (36 . 4) mililitros por minuto
d) 81/(16 . 36) mililitros por minuto
e) (4 . 6)/9 mililitros por minuto
Resposta Questão 1
Letra b). Dados fornecidos pelo exercício:
- Moléculas perdidas de hidrogênio = 6.104 a cada segundo
- Tempo necessário para o reservatório com oxigênio perder 6.104 moléculas = ?
1º Passo: Calcular a massa molar do gás oxigênio.
Para isso, devemos multiplicar a massa atômica do elemento pela sua quantidade de átomos na fórmula:
Massa molar do O2 = 2.16
Massa molar do O2 = 32 g/mol
2º Passo: Calcular a massa molar do gás hidrogênio.
Para isso, devemos multiplicar a massa atômica do elemento pela sua quantidade de átomos na fórmula:
Massa molar do H2 = 2.1
Massa molar do H2 = 2 g/mol
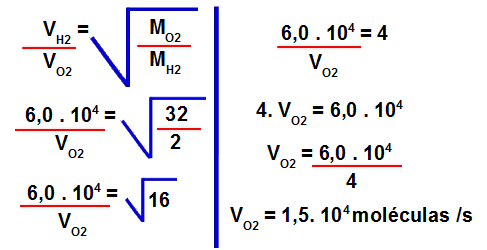
3º Passo: Determinar a velocidade de efusão do gás oxigênio.
Para isso, devemos utilizar os valores fornecidos na fórmula para cálculo da velocidade de efusão:
4º Passo: Determinar o tempo necessário para sair do reservatório com gás oxigênio o mesmo número de moléculas que saíram do reservatório com gás hidrogênio.
Para isso, basta utilizar a seguinte regra de três:
Resposta Questão 2
Letra c). Dados fornecidos pelo exercício:
- Velocidade de efusão do gás hélio (He) = 6,75 km/min;
- Massa molar do gás hélio (He) = 4 g/mol;
- Velocidade de efusão do gás oxigênio (O2) = ? km/h.
1º Passo: Calcular a massa molar do gás oxigênio.
Para isso, devemos multiplicar a massa atômica do elemento pela sua quantidade de átomos na fórmula:
Massa molar do O2 = 2.16
Massa molar do O2 = 32 g/mol
2º Passo: Determinar a velocidade de efusão do gás oxigênio.
Para isso, devemos utilizar os valores fornecidos na fórmula para cálculo da velocidade de efusão:#
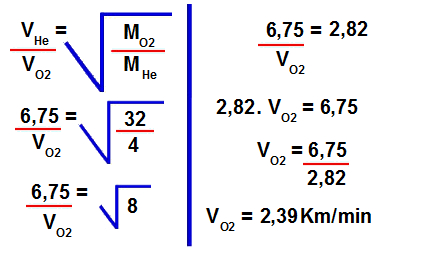
3º Passo: Transformar a velocidade de Km/min para Km/h.
Para isso, basta utilizar a seguinte regra de três:
Resposta Questão 3
Letra d). Dados fornecidos pelo exercício:
- Velocidade de efusão do gás hélio (He) = 6,0 . 103 km/h
- Massa molar do gás hélio (He) = 4 g/mol
- Velocidade de efusão do gás dióxido de enxofre (SO2) = ? km/h
1º Passo: Calcular a massa molar do dióxido de enxofre.
Para isso, devemos multiplicar a massa atômica do elemento pela sua quantidade de átomos na fórmula e, em seguida, somar os resultados:
Massa molar do SO2 = 1.32 + 2.16
Massa molar do SO2 = 32 + 32
Massa molar do SO2 = 64 g/mol
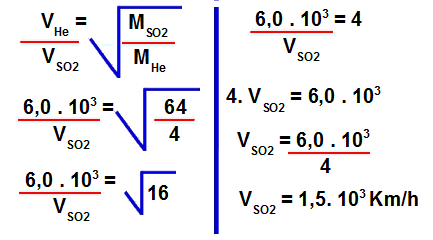
2º Passo: Determinar a velocidade de efusão do dióxido de enxofre.
Para isso, devemos utilizar os valores fornecidos na fórmula para cálculo da velocidade de efusão:
3º Passo: Encontrar a proporção de quantas vezes a velocidade do gás hélio é maior que a velocidade do gás dióxido de enxofre.
Para isso, basta dividir a velocidade de efusão do hélio pela velocidade de difusão do dióxido de enxofre:
Portanto, a velocidade de efusão do hélio é quatro vezes maior que a velocidade de efusão do dióxido de enxofre.
Resposta Questão 4
Letra a). Dados fornecidos pelo exercício:
- Velocidade de efusão do gás metano (CH4) = 36 mL/min
- Velocidade de efusão do gás brometo de hidrogênio (HBr) = ? km/h
1º Passo: Calcular a massa molar do brometo de hidrogênio.
Para isso, devemos multiplicar a massa atômica do elemento pela sua quantidade de átomos na fórmula e, em seguida, somar os resultados:
Massa molar do HBr = 1.1 + 1.80
Massa molar do HBr = 1 + 80
Massa molar do HBr = 81 g/mol
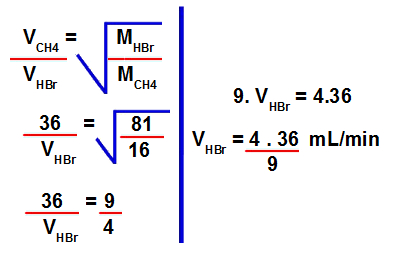
2º Passo: Determinar a velocidade de efusão do brometo de hidrogênio.
Para isso, devemos utilizar os valores fornecidos na fórmula para cálculo da velocidade de efusão: