Questão 1
(PUC-SP) Na figura a seguir, tem-se o prisma reto ABCDEF, no qual DE = 6 cm, EF = 8 cm e DE é perpendicular a EF.
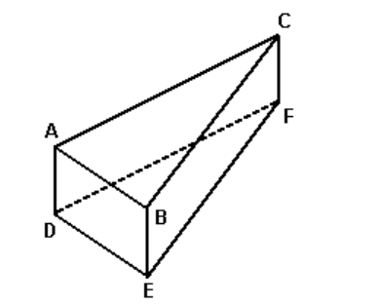
Se o volume desse prisma é 120 cm3, a sua área total, em centímetros quadrados, é:
a) 144
b) 156
c) 160
d) 168
e) 172
Questão 2
(PUC-SP) Um tanque de uso industrial tem a aforma de um prisma cuja base é um trapézio isósceles. Na figura a seguir, são dadas as dimensões, em metros, do prisma:
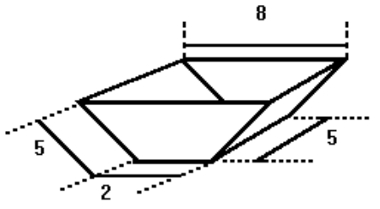
O volume desse tanque, em metros cúbicos, é:
a) 50
b) 60
c) 80
d) 100
e) 120
Questão 3
Um copo tem o formato de prisma cuja base é um octógono regular. As arestas da base desse copo medem 2 centímetros e ele possui 15 centímetros de altura. Sabendo que o apótema desse octógono mede aproximadamente 2,5 cm, qual é o volume desse copo em centímetros cúbicos?
a) 120,6
b) 200,6
c) 207,6
d) 300
e) 0,6
Questão 4
Um bloco retangular possui como base um retângulo com área de 120 cm2. Sabendo que o volume desse bloco é de 480 cm3, qual é sua altura em centímetros?
a) 4
b) 5
c) 6
d) 7
e) 8
Resposta Questão 1
O volume de um prisma é a área de sua base multiplicada por sua altura. A base desse prisma é um triângulo retângulo. Podemos dizer que a base e a altura desse triângulo medem 8 cm e 6 cm. Assim, o volume desse prisma é dado pela seguinte expressão:
6·8·EB = 120
2
48·EB = 120
2
24·EB = 120
EB = 120
24
EB = 5 cm.
Para calcular a área de um prisma, é necessário calcular as áreas de todas as suas faces e somá-las. Na face ADCF desse prisma, ainda não existe medida para o lado DF, que é importante para o cálculo da área dessa face. Esse lado pode ser descoberto pelo teorema de Pitágoras, uma vez que DE é perpendicular a EF. Assim, DF é a hipotenusa do triângulo em que esses lados são catetos:
DF2 = 82 + 62
DF2 = 64 + 36
DF = √100
DF = 10 cm
A área de ADCF, portanto, é: 10·5 = 50 cm2. A área de BCEF é 8·5 = 40 cm2. A área de ABDE é 6·5 = 30 cm2. As áreas dos triângulos medem 24 cm2 cada. Assim, a área total da figura é:
24 + 24 + 30 + 40 + 50 = 168 cm2
Gabarito: letra D.
Resposta Questão 2
O trapézio, base desse prisma, possui as seguintes medidas:
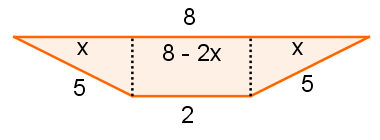
Observe que 8 – 2x = 2, logo, 2x = 8 – 2 e, assim, 2x = 6. Portanto, x = 3. Como x é igual a 3, podemos descobrir a altura do trapézio usando o teorema de Pitágoras:
52 = 32 + h2
25 = 9 + h2
h2 = 25 – 9
h2 = 16
h = √16
h = 4
O volume do tanque é a área da base multiplicada por sua altura, pois o tanque tem formato de prisma. Assim, a área da base e o volume do tanque são:
A = (B + b)h
2
A = (8 + 2)4
2
A = 10·2
A = 20 m2
V = 20·h
V = 20·5
V = 100 m3
Gabarito: letra D.
Resposta Questão 3
Um octógono regular pode ser dividido em 8 triângulos isósceles, cada um deles com base de 2 centímetros e 2,5 cm de altura. Se a área do triângulo isósceles é:
A = bh
2
Então, a área da base é oito vezes a área do triângulo isósceles.
A = 8bh
2
A = 8·2·2,5
4
A = 40
2
AB = 20 cm2
Multiplicando a área da base pela altura do copo, teremos:
V = 15·20
V = 300 cm3
Gabarito: letra D.
Resposta Questão 4
O volume de um prisma é a área da base multiplicada pela altura. Os blocos retangulares são prismas, por isso, basta calcular:
V = Ah
480 = 120h
h = 480
120
h = 4 centímetros.
Gabarito: letra A.



