Questão 1
A respeito da definição e dos elementos de um trapézio, assinale a alternativa correta:
a) Trapézios são quadriláteros que possuem dois pares de lados paralelos.
b) Trapézios são figuras planas formadas por quatro lados e um par de lados adjacentes paralelos.
c) Todo trapézio possui diagonais congruentes.
d) Trapézios são quadriláteros que possuem um par de lados opostos paralelos.
Questão 2
Sabendo que as diagonais de um trapézio medem 7x – 125 e 4x + 43, qual é o valor de x para que esse trapézio seja isósceles?
a) 56
b) 128
c) 168
d) 199
e) 256
Questão 3
Calcule a área da parte colorida da figura a seguir sabendo que ela representa um retângulo de 8 metros de largura por 4 metros de comprimento e que dela foi extraído um trapézio que deixou o espaço branco à esquerda.
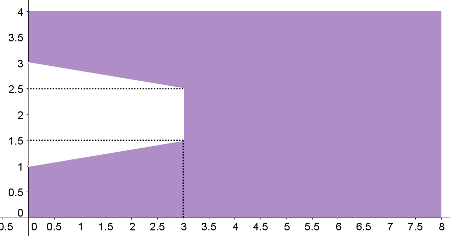
a) 32 m2
b) 4,5 m2
c) 27,5 m2
d) 32,5 m2
e) 84 m2
Questão 4
Um trapézio possui ângulos internos com as seguintes medidas: 2x, 2x, x e x. Qual é a medida de cada ângulo desse trapézio?
a) Todos medem 540°.
b) Todos medem 90°.
c) Dois ângulos de 60° e dois de 360°.
d) Dois ângulos de 60° e dois de 120°.
e) todos medem 60°.
Resposta Questão 1
a) Incorreta!
Os trapézios são quadriláteros que possuem um par de lados opostos paralelos.
b) Incorreta!
Os trapézios não possuem um par de lados adjacentes paralelos, mas, sim, um par de lados opostos paralelos.
c) Incorreta!
Apenas os trapézios isósceles possuem diagonais congruentes.
d) Correta!
Gabarito: letra D.
Resposta Questão 2
Um trapézio isósceles possui diagonais congruentes. Assim, o valor de x que faz com que esse trapézio seja isósceles pode ser encontrado pela equação:
7x – 125 = 4x + 43
7x – 4x = 43 + 125
3x = 168
x = 168
3
x = 56
Gabarito: letra A.
Resposta Questão 3
Para resolver esse problema, basta calcular a área do retângulo e dela subtrair a área do trapézio, que também deve ser calculada.
A área do retângulo é obtida pela multiplicação de sua base por sua altura. Assim, temos:
AR = 8·4
AR = 32 m2
A área do trapézio depende do comprimento de sua altura e de suas bases. A base maior é o segmento que está sobre o eixo y e vai de 1 a 3, portanto, mede 2 metros. A base menor contém indicações de que seu comprimento é igual ao do segmento que vai de 1,5 a 2,5. Mede, portanto, 1 metro. A altura é a distância do eixo y até o topo do trapézio, logo, mede 3 metros. Substituindo esses valores na fórmula da área do trapézio, temos:
AT = (B + b)h
2
AT = (2 + 1)3
2
AT = (3)3
2
AT = 9
2
AT = 4,5 m2
Agora basta subtrair da área do retângulo a área do trapézio:
A = 32 – 4,5 = 27,5 m2
Gabarito: letra C.
Resposta Questão 4
A soma dos ângulos internos de um polígono (os trapézios também são polígonos) é obtida pela seguinte expressão:
S = (n – 2)180
*n é o número de lados do polígono. Para os trapézios, a soma é:
S = (4 – 2)180
S = (2)180
S = 360°
Agora basta somar os ângulos internos do trapézio em questão e igualar essa soma a 360°. Observe:
2x + 2x + x + x = 360
6x = 360
x = 360
6
x = 60
Assim, os ângulos internos desse trapézio são: 60°, 60°, 120° e 120°.
Gabarito: letra D.



