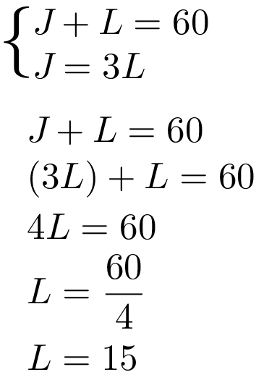Questão 1
A soma das idades de Joaquim e Lúcio é 60 anos. Sabendo que a idade de Joaquim é o triplo da idade de Lúcio, qual é a idade de cada um deles?
a) 15 e 45 anos
b) 30 e 30 anos
c) 20 e 40 anos
d) 5 e 55 anos
e) 10 e 50 anos
Questão 2
João cria 60 animais em sua fazenda. Alguns deles eram vacas, outros eram galinhas. Sabendo que o total de patas registradas em uma inspeção foi de 220, quantas vacas João cria?
a) 40 vacas
b) 50 vacas
c) 10 vacas
d) 30 vacas
e) 20 vacas
Questão 3
Uma fábrica produz 240 peças de metal, algumas delas medindo 30 e outras medindo 40 centímetros. Sabendo que o comprimento total das peças produzidas é igual a 7600 centímetros, quantas peças de 30 centímetros foram produzidas?
a) 100
b) 150
c) 200
d) 250
e) 300
Questão 4
Qual é o par ordenado que resolve o sistema a seguir?
.jpg)
a) (1, 4)
b) (2, 6)
c) (40, 10)
d) (20, 30)
e) (10, 40)
Resposta Questão 1
Representando a idade de Lúcio por L e a de Joaquim por J, podemos construir as seguintes equações:
J + L = 60 e
J = 3L
Com essas duas equações, é possível montar o sistema a seguir, que será resolvido pelo método da comparação:
Sabendo que a idade de Lúcio é 15 anos e que a idade de Joaquim é o triplo da idade de Lúcio, teremos:
J = 3L
J = 3·15
J = 45 anos
Alternativa A
Resposta Questão 2
Sejam as galinhas representadas pela letra G e as vacas pela letra V, podemos montar as duas equações a seguir:
G + V = 60
2G + 4V = 220
Com essas equações, é possível montar o seguinte sistema, que será resolvido usando o método da substituição.
Observe o valor algébrico de G, na primeira equação:
G + V = 60
G = 60 – V
Substitua esse valor na segunda:
2G + 4V = 220
2(60 – V) + 4V = 220
120 – 2V + 4V = 220
2V = 220 – 120
2V = 100
V = 100
2
V = 50
Como queríamos o número de vacas, a solução do exercício é a letra B.
Resposta Questão 3
Seja x o número de peças de 30 cm e y o número de peças de 40 cm, as equações que podem ser extraídas do problema são:
x + y = 240
30x + 40y = 7600
Com essas equações, é possível montar o seguinte sistema:
Primeiramente, encontraremos o valor algébrico da incógnita y, na primeira equação:
x + y = 240
y = 240 – x
Em seguida, substitua o valor encontrado na segunda equação:
30x + 40y = 7600
30x + 40(240 – x) = 7600
30x + 9600 – 40x = 7600
30x – 40x = 7600 – 9600
– 10x = – 2000 (– 1)
10x = 2000
x = 2000
10
x = 200 peças de 30 cm.
Como o exercício pede o número de peças de 30 cm, a solução é a alternativa C.
Resposta Questão 4
Da primeira equação, encontraremos o valor algébrico de y:
2x + y = 60
y = 60 – 2x
Depois, substituiremos esse valor na segunda equação:
x + 6y = 250
x + 6(60 – 2x) = 250
x + 360 – 12x = 250
– 11x = 250 – 360
– 11x = – 110 (– 1)
11x = 110
x = 110
11
x = 10
Sabendo que x é igual a 10, substitua esse valor em qualquer uma das equações:
2x + y = 60
2·10 + y = 60
20 + y = 60
y = 60 – 20
y = 40
O par ordenado é (10, 40).
Alternativa E.