Questão 1
(ENEM 2008) O tangram é um jogo oriental antigo, uma espécie de quebra-cabeça, constituído de sete peças: 5 triângulos retângulos e isósceles, 1 paralelogramo, e 1 quadrado. Essas peças são obtidas recortando-se um quadrado de acordo com o esquema da figura 1. Utilizando-se todas as sete peças, é possível representar uma grande diversidade de formas, como as exemplificadas nas figuras 2 e 3.
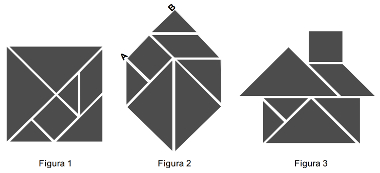
Se o lado AB do hexágono mostrado na figura 2 mede 2 cm, então a área da figura 3, que representa uma “casinha”, é igual a
a) 4 cm2
b) 8 cm2
c) 12 cm2
d) 14 cm2
e) 16 cm2
Questão 2
A respeito dos quadrados, qual das alternativas abaixo é incorreta.
a) Os quadrados são paralelogramos que possuem lados e ângulos congruentes.
b) Os quadrados são retângulos com lados que possuem as mesmas medidas.
c) Os quadrados são losangos com ângulos que possuem as mesmas medidas.
d) Todo losango também é um quadrado.
e) Todo quadrado também é um losango.
Questão 3
Das alternativas abaixo, que discorrem sobre os quadrados, assinale aquela que for correta.
a) Os quadrados possuem diagonais que se encontram em seus pontos médios, são perpendiculares, mas não são congruentes.
b) Os quadrados possuem ângulos externos indeterminados.
c) A área do quadrado pode ser calculada pelo produto de suas diagonais dividido por 2.
d) O perímetro do quadrado é igual ao quadrado do seu lado.
e) A área do quadrado é igual à soma das medidas dos seus lados.
Questão 4
Qual o perímetro de um quadrado que possui uma das diagonais medindo a raiz quadrada de 72 cm?
a) 24 cm
b) 25 cm
c) 28 cm
d) 36 cm
e) 6 cm
Resposta Questão 1
Observe que o lado AB é formado pelos lados de um quadrado e um triângulo, que podem ser encontrados na diagonal do quadrado na figura 1 (o quadrado que foi dividido para formar o tangram). Sabendo que as diagonais de um quadrado se encontram em seus pontos médios, essa diagonal mede 4 cm. Além disso, as diagonais do quadrado são congruentes. Logo, a outra diagonal também mede 4 cm. Sabendo que todo quadrado também é um losango, utilizaremos a fórmula para calcular a área do losango para descobrir a área do quadrado da figura 1 (obs.: estamos falando do quadrado grande, que foi dividido para formar o tangram).
A = D·d
2
A = 4·4
2
A = 16
2
A = 8 cm2
Gabarito, alternativa B.
Resposta Questão 2
a) Correta!
Essa é exatamente a definição de quadrado.
b) Correta!
Todo quadrado também é um retângulo. Como os quadrados possuem lados com medidas iguais, então a afirmação se faz verdadeira.
c) Correta!
Todo quadrado também é um losango. Como os quadrados possuem apenas ângulos internos retos, então a afirmação se faz verdadeira.
d) Incorreta!
Nem todo losango possui ângulos internos retos, o que é indispensável para que a figura seja considerada um quadrado.
e) Correta!
Todo quadrado é um losango, pois os quadrados possuem os quatro lados congruentes, o que é a própria definição de losango.
Gabarito, alternativa D.
Resposta Questão 3
a) Incorreta!
Os quadrados possuem diagonais que se encontram em seus pontos médios, perpendiculares e congruentes.
b) Incorreta!
Os Ângulos externos de um quadrado também medem 90°.
c) Correta!
Exatamente como se calcula a área de um losango. Como todo quadrado é losango, então a afirmativa está correta.
d) Incorreta!
O perímetro do quadrado é a soma dos seus lados.
e) Incorreta!
A área do quadrado é o produto entre base e altura, o que acaba se tornando a medida do lado elevada ao quadrado.
Gabarito, alternativa C.
Resposta Questão 4
A diagonal de um quadrado o divide em dois triângulos isósceles e retângulos, cujo ângulo reto é oposto à diagonal. Logo, a diagonal é hipotenusa e os outros dois lados catetos desse triângulo. Sabendo que esses dois lados são iguais, pois são os lados do quadrado, poderemos fazer os seguintes cálculos:
Seja x o lado do quadrado. Sabendo que x também será o lado do triângulo e que 72 será sua hipotenusa, pelo teorema de Pitágoras teremos:
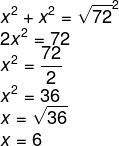
Gabarito, alternativa E.



