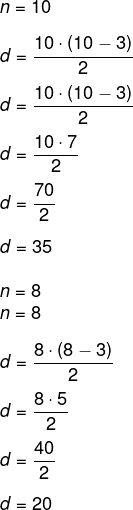Questão 1
Existe um polígono que possui o número de lados igual ao número de diagonais. O nome desse polígono é:
A) quadrado.
B) pentágono.
C) hexágono.
D) heptágono.
E) octógono.
Questão 2
O polígono que possui 35 diagonais é conhecido como:
A) hexágono.
B) heptágono.
C) octógono.
D) eneágono.
E) decágono.
Questão 3
Das alternativas a seguir, marque aquela que é incorreta.
A) A soma dos ângulos internos de um quadrilátero é sempre igual a 360º.
B) Todo polígono convexo possui diagonal.
C) Um polígono é conhecido como regular quando ele possui todos os lados e ângulos congruentes.
D) Um polígono é convexo quando todos os seus ângulos internos são menores que 180º.
E) O pentágono possui 5 diagonais.
Questão 4
Sabendo que o polígono a seguir é regular, o valor de cada um dos seus ângulos internos é:
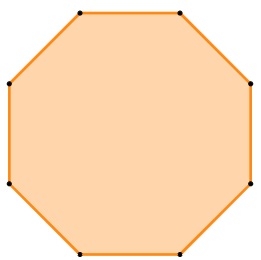
A) 540º.
B) 1080º.
C) 900º.
D) 175º.
E) 135º.
Questão 5
O número de lados de um polígono cuja soma dos ângulos internos é igual a 720º é:
A) 5.
B) 6.
C) 7.
D) 8.
E) 10.
Questão 6
(Mackenzie-SP) Os ângulos externos de um polígono regular medem 20°. Então, o número de diagonais desse polígono é:
A) 90.
B) 104.
C) 119.
D) 135.
E) 152.
Questão 7
Os ângulos internos de um triângulo são proporcionais aos números 3, 5 e 7. Sendo assim, a medida do maior ângulo será igual a:
A) 12º.
B) 84º.
C) 60º.
D) 36º.
E) 96º.
Questão 8
(PUC-RJ) Os ângulos internos de um quadrilátero medem 3x – 45, 2x + 10, 2x + 15 e x + 20 graus. O menor ângulo mede:
A) 90°.
B) 65°.
C) 45°.
D) 105°.
E) 80°.
Questão 9
(IFTM) Uma porca sextavada é um elemento de fixação utilizado em conjunto com os parafusos. Ela possui esse nome porque seu formato é associado a um polígono regular de seis lados. A figura mostra uma representação geométrica desse tipo de porca.
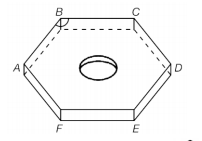
Qual é a medida do ângulo ABC?
A) 100º.
B) 108º.
C) 120º.
D) 135º.
E) 144º.
Questão 10
A diferença entre o número de diagonais de um polígono que possui 10 lados e um polígono que possui 8 lados é igual a:
a) 10.
b) 12.
c) 14.
d) 15.
e) 18.
Questão 11
Sobre o conceito de polígono convexo e não convexo, marque a alternativa correta.
A) Um polígono é convexo quando todos os seus lados e também os seus ângulos são congruentes, ou seja, possuem a mesma medida.
B) Um polígono é convexo quando possui diagonais.
C) Um polígono é convexo quando, dados quaisquer dois pontos (A e B) pertencentes ao polígono, o segmento de reta AB também pertence ao polígono.
D) Um polígono é convexo quando a quantidade de diagonais é igual à quantidade de lados.
Questão 12
Um conceito importante ao estudar polígonos é o de polígono regular. Dos polígonos a seguir, indique aquele que é sempre regular.
A) Retângulo
B) Losango
C) Trapézio
D) Triângulos isósceles
E) Quadrado
Resposta Questão 1
Alternativa B.
Utilizando a fórmula da diagonal, temos que d = n.
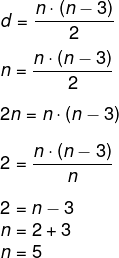
O polígono que possui 5 lados é o pentágono.
Resposta Questão 2
Alternativa E.
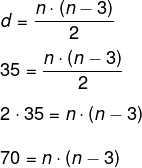
Sabemos que os divisores de 70 são:
D(70) = 1, 2, 5, 7,10,14, 35, 70.
Dos valores possíveis, o único que faz com que a equação seja verdadeira é n = 10, pois:
10 · (10 – 3 ) = 10 · 7 = 70
Resposta Questão 3
Alternativa B. O único polígono que não possui diagonal é o triângulo, o que torna a alternativa B a única incorreta.
Resposta Questão 4
Alternativa E. Esse polígono possui oito lados. Para calcular o valor de cada um dos ângulos, vamos utilizar a fórmula da soma dos ângulos internos.
Si = (n – 2) · 180
Si = ( 8 – 2) · 180
Si = 6 · 180
Si = 1080
Como o polígono é regular, todos os ângulos são congruentes, então a medida de cada um é igual a:
1.080 : 8 = 135º
Resposta Questão 5
Alternativa B.
Utilizando a fórmula da soma dos ângulos internos, temos que:
Si = ( n – 2 ) 180
720 = ( n – 2) 180
720 / 180 = n – 2
4 = n – 2
n = 4+2
n = 6
Resposta Questão 6
Alternativa D. A soma dos ângulos externos de um polígono é sempre igual a 360º, então, para descobrir o número de lados, faremos 360 : 20 = 18.
Como esse polígono possui 18 lados, então basta substituir na fórmula das diagonais.
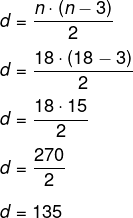
Resposta Questão 7
Alternativa B.
Sabendo que a soma dos ângulos internos é sempre igual a 180º, sejam a, b e c os ângulos internos do triângulo, então:
a + b + c = 180
Por proporção, temos que:
a = 3k
b = 5k
c = 7k
Assim sendo, podemos escrever que:
3k + 5k + 7k = 180
15k = 180
k = 180/ 15
k =12
O maior ângulo é 7k → 7 ·12 = 84.
Resposta Questão 8
Alternativa B.
A soma dos ângulos internos de um quadrilátero é sempre igual a 360º.
3x – 45 + 2x + 10 + 2x + 15 + x + 20 = 360
8x – 10 = 360
8x = 360
x = 360 : 8
x = 45
O menor ângulo é 45 + 20 = 65º.
Resposta Questão 9
Alternativa C.
Analisando a figura, é possível perceber que ela possui 6 lados. Então, utilizando a fórmula da soma dos ângulos internos, temos que:
Si = ( n – 2 ) 180º
Si = (6 – 2 ) 180º
Si = 4 · 180º
Si = 720º
A medida de um ângulo é, portanto, 720 : 6 = 120º.
Resposta Questão 12
Alternativa E. Para ser regular, os ângulos e os lados têm que ser congruentes. Dos polígonos listados, o único que é regular é o quadrado, que possui lados e ângulos congruentes.