Questão 1
A respeito da definição de polígonos semelhantes e congruentes, assinale a alternativa verdadeira:
a) Dois polígonos que possuem lados com medidas iguais são semelhantes.
b) Dois polígonos que possuem ângulos congruentes são semelhantes.
c) Um polígono é convexo e o outro não. Esses dois polígonos são semelhantes.
d) Dois polígonos que possuem lados correspondentes proporcionais e ângulos correspondentes congruentes são semelhantes.
e) Apenas triângulos podem ser considerados semelhantes.
Questão 2
Dois polígonos ABCD e EFGH são semelhantes. Supondo que os ângulos internos do polígono ABCD sejam todos iguais, qual a medida do ângulo H do polígono EFGH?
a) 30°
b) 45°
c) 60°
d) 90°
e) 120
Questão 3
A respeito das propriedades dos polígonos semelhantes, assinale a alternativa correta:
a) As diagonais de polígonos semelhantes são proporcionais, na mesma razão estabelecida entre os polígonos.
b) As diagonais de polígonos semelhantes são proporcionais, na razão inversa à estabelecida entre os polígonos.
c) As diagonais de polígonos semelhantes não são proporcionais.
d) Os perímetros de polígonos semelhantes são proporcionais, na razão inversa à estabelecida entre os lados dos polígonos.
e) Os perímetros de polígonos semelhantes não são proporcionais.
Questão 4
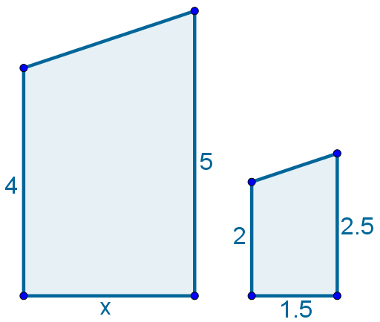
Determine a medida x do polígono abaixo, sabendo que os polígonos da imagem são semelhantes.
a) 3
b) 4
c) 5
d) 6
e) 7
Resposta Questão 1
Dois polígonos são semelhantes quando os seus lados correspondentes forem proporcionais e seus ângulos correspondentes forem congruentes. Assim sendo, a alternativa correta é a letra D. Dois polígonos que possuem apenas as medidas de lados correspondentes iguais não podem ser semelhantes, pois não há garantias sobre seus ângulos.
O mesmo vale para os ângulos congruentes de dois polígonos, já que não existe garantia para seus lados.
Quando um polígono é convexo e outro não, pelo menos um dos ângulos internos de um desses dois polígonos não é congruente ao ângulo correspondente do outro.
Por fim, polígonos com qualquer número de lados podem ser semelhantes, desde que seus lados correspondentes sejam proporcionais e seus ângulos correspondentes sejam congruentes.
Gabarito: Alternativa D
Resposta Questão 2
Como os dois polígonos são semelhantes, seus ângulos correspondentes têm a mesma medida. Como todos os ângulos do polígono ABCD são iguais, o ângulo H terá a medida de qualquer um deles. Para descobrir a medida de um dos ângulos de ABCD, deve-se pensar o seguinte: ABCD é um quadrilátero, cuja soma dos ângulos internos é dada por:
S = (n – 2)180
S = (4 – 2)180
S = (2)180
S = 360°
Como os ângulos internos desse polígono são todos iguais, então, basta dividir 360° por 4 para encontrar a medida de cada ângulo e, consequentemente, a medida do ângulo H.
360/4 = 90°
Gabarito: Alternativa D
Resposta Questão 3
A propriedade em questão garante que diagonais e perímetros de polígonos semelhantes sejam proporcionais na mesma razão estabelecida entre os lados dos polígonos. Assim sendo, a alternativa correta é a letra A.
Gabarito: Alternativa A
Resposta Questão 4
Se os dois polígonos são semelhantes, basta montar uma proporção envolvendo seus lados para descobrir o valor de x:
x = 4
1,5 2
2x = 4·1,5
2x = 6
x = 6
2
x = 3
Gabarito: Alternativa A