Questão 1
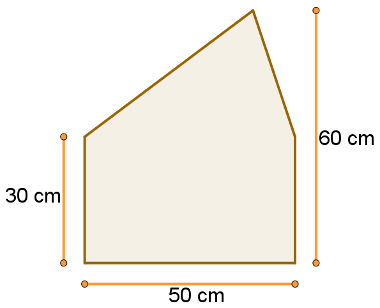
Calcule a medida da área do pentágono na figura a seguir, considerando as medidas que foram colocadas nela.A
a) 750 cm2
b) 1500 cm2
c) 2250 cm2
d) 3000 cm2
e) 9000 cm2
Questão 2
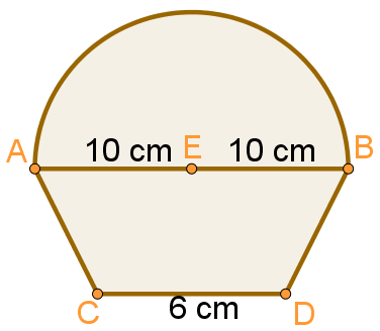
Qual é a área da figura a seguir, sabendo que a distância entre o ponto E e a base da figura CD é igual a 10 cm?
a) 100 cm2
b) 187 cm2
c) 287 cm2
d) 387 cm2
e) 487 cm2
Questão 3
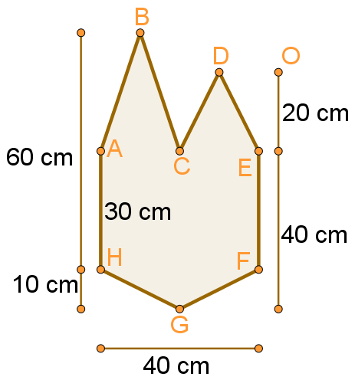
Calcule a área da figura a seguir, sabendo que os pontos A, C e E são retilíneos, que o ponto C é ponto médio do segmento AE e que a reta que os contém é paralela à reta que contém os pontos H e F.
a) 200 cm2
b) 300 cm2
c) 1000 cm2
d) 1900 cm2
e) 2200 cm2
Questão 4
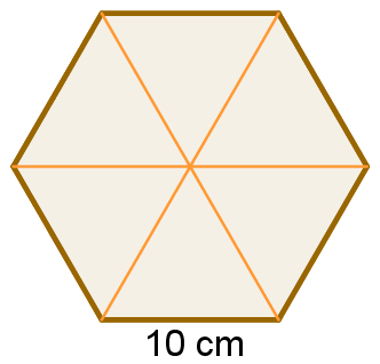
Qual é a área de um hexágono regular de lado 10 cm?
a) 150√3 cm2
b) 50√3 cm2
c) 10√3 cm2
d) 5√3 cm2
e) 15√3 cm2
Resposta Questão 1
Perceba que essa figura é formada por um triângulo sobre um retângulo. Para calcular sua área, basta somar a área do triângulo e do retângulo. Observe que o retângulo tem base igual a 50 cm e que sua altura é igual a 30 cm. A base do triângulo também mede 50 cm e o que sobra para sua altura é 30 cm, uma vez que a altura total da figura é de 60 cm e a altura do retângulo mede 30 cm.
Então, a área do retângulo é:
Ar = b·h = 50·30 = 1500 cm2
A área do triângulo é:
At = b·h = 50·30 = 1500 = 750 cm2
2 2 2
E a área do pentágono é a soma das áreas do triângulo e do retângulo:
Ar + At = 1500 + 750 = 2250 cm2
Alternativa C
Resposta Questão 2
Observe que a parte de cima dessa figura é um semicírculo (metade de um círculo) de raio 10 cm, e a parte de baixo é um trapézio, com base maior igual a 20 cm, base menor igual a 6 cm e altura igual a 10 cm (pois a altura é igual à distância entre o ponto E e a base CD).
A área do semicírculo é igual à metade da área do círculo, logo:
Asc = πr2
2
Asc = 3,14·102
2
Asc = 3,14·100
2
Asc = 314
2
Asc = 157 cm2
A área do trapézio é dada pela fórmula:
At = (B + b)·h
2
At = (20 + 6)·10
2
At = (26)·10
2
At = 260
2
At = 130 cm2
A área da figura da imagem é igual à soma das áreas do semicírculo e do trapézio:
Asc + At = 157 + 130 = 287 cm2
Alternativa C
Resposta Questão 3
Se os pontos A, C e E são retilíneos e a reta que os contém é paralela à reta que contém os pontos H e F, então é possível dividir essa figura em três triângulos e um retângulo. As medidas dos triângulos serão:
Triângulo ABC: 30 cm de altura e 20 cm de largura. Triângulo CDE: 20 cm de altura e 20 cm de largura. Triângulo HFG: 10 cm de altura e 40 cm de largura.
As medidas do retângulo são: 30 cm de altura e 40 cm de base.
As áreas dos triângulos são:
A1 = b·h
2
A1 = 20·30
2
A1 = 600
2
A1 = 300 cm2
A2 = b·h
2
A2 = 20·20
2
A2 = 400
2
A2 = 200 cm2
A3 = b·h
2
A3 = 40·10
2
A3 = 400
2
A3 = 200 cm2
A área do retângulo é:
Ar = b·h
Ar = 40·30
Ar = 1200 cm2
A área total da figura é:
A = 300 + 200 + 200 + 1200 = 1900 cm2
Alternativa D
Resposta Questão 4
Um hexágono regular pode ser dividido em 6 triângulos, como mostra a figura a seguir. Esses triângulos, por sua vez, são congruentes, uma vez que o hexágono é regular. Obtendo a área de um desses triângulos, basta multiplicá-la por 6.
Para isso, será necessário descobrir sua altura, que também é o apótema do hexágono regular. A fórmula para calcular o apótema do hexágono regular é:
a = r√3
2
Nessa fórmula, r é o raio do polígono. Como se trata de um hexágono regular, o raio do polígono é igual ao lado l do polígono. Então, podemos escrever:
a = l√3
2
Substituindo o valor do lado do polígono, teremos:
a = 10√3
2
a = 5√3
Essa é a altura de um dos triângulos, nos quais o hexágono foi dividido.
A área desse triângulo é:
AT = b·h
2
AT = 10·5√3
2
AT = 50√3
2
AT = 25√3 cm2
Sendo a área de um triângulo igual a 25√3 cm2 e o hexágono regular composto por 6 triângulos, teremos:
AHr = 6 (25√3) cm2
AHr = 150√3 cm2
Alternativa A