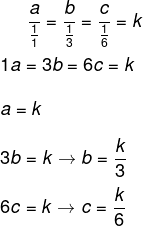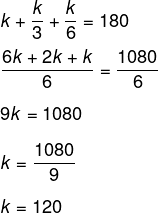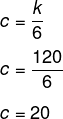Questão 1
Um automóvel gasta 2 horas para realizar um determinado percurso. Sabendo que outro automóvel fez o mesmo percurso a uma velocidade média de 60 km/h e levou 3 horas, qual foi a velocidade do primeiro automóvel?
A) 50 km/h
B) 65 km/h
C) 70 km/h
D) 80 km/h
E) 90 km/h
Questão 2
Sabemos que a densidade de uma substância é calculada pela razão entre a massa e o volume. Se determinada substância possui 2 cm³ de volume, com densidade de 100 g/cm³, tendo a mesma massa, qual deve ser o volume de uma outra substância para que a sua densidade seja de 80 g/cm³?
A) 2,2 cm³
B) 2,5 cm³
C) 2,8 cm³
D) 3,0 cm³
E) 3,4 cm³
Questão 3
Um ângulo raso foi dividido em três partes inversamente proporcionais aos números 1, 3 e 6. Nessas condições, o menor ângulo mede:
A) 20º
B) 45º
C) 60º
D) 90º
E) 120º
Questão 4
(Objetiva 2015) Em determinado dia de trabalho, três auxiliares administrativos arquivaram 1324 processos ao todo. Sabendo-se que a quantidade de processos que cada auxiliar arquivou é inversamente proporcional às suas idades, que são 28, 30 e 54 anos, respectivamente, assinalar a alternativa CORRETA:
A) O auxiliar administrativo com 28 anos arquivou 542 processos.
B) O auxiliar administrativo com 30 anos arquivou 504 processos.
C) O auxiliar administrativo com 54 anos arquivou 282 processos.
D) O auxiliar administrativo com 28 anos arquivou 544 processos.
Questão 5
Para a realização de uma obra, foram contratados 6 operários que levaram 18 dias para executar a metade desse trabalho. Se forem contratados mais 3 funcionários, qual será o tempo total gasto na obra?
A) 12 dias
B) 24 dias
C) 28 dias
D) 30 dias
E) 36 dias
Questão 6
Uma herança de R$ 2.950.000 foi dividida aos três herdeiros de forma inversamente proporcional aos números 2, 5 e 7. Sendo assim, o herdeiro que recebeu a maior parte herdou um total de:
A) R$ 1.950.000
B) R$ 2.100.000
C) R$ 1.800.000
D) R$ 1.750.000
E) R$ 900.000
Questão 7
(Enem 2019) Para contratar três máquinas que farão o reparo de vias rurais de um município, a prefeitura elaborou um edital que, entre outras cláusulas, previa:
• Cada empresa interessada só pode cadastrar uma única máquina para concorrer ao edital;
• O total de recursos destinados para contratar o conjunto das três máquinas é de R$ 31 000;
• O valor a ser pago a cada empresa será inversamente proporcional à idade de uso da máquina cadastrada pela empresa para o presente edital.
As três empresas vencedoras do edital cadastraram máquinas com 2, 3 e 5 anos de idade de uso.
Quanto receberá a empresa que cadastrou a máquina com maior idade de uso?
A) R$ 3100
B) R$ 6000
C) R$ 6200
D) R$ 15.000
E) R$ 15.500
Questão 8
Em uma fábrica, há três máquinas e a produção é inversamente proporcional ao tempo de uso das máquinas em meses. Sabendo que as três possuem, respectivamente, 28, 32 e 36 meses de uso, e que, em um determinado tempo, as máquinas produziram, ao todo, 3820 peças, a quantidade de peças produzidas pela máquina mais nova é igual a:
A) 860
B) 900
C) 1050
D) 1120
E) 1440
Questão 9
Analisando as alternativas abaixo, marque aquela em que as grandezas se relacionam de forma inversamente proporcional.
A) A distância percorrida por um veículo e o tempo de percurso em uma velocidade constante.
B) A idade da pessoa e o seu salário mensal.
C) A vazão da água de uma mangueira e o tempo que ela leva para preencher um reservatório.
D) A quantidade de concreto produzido e a quantidade de cimento necessária.
E) O número de acertos em uma prova e a nota obtida pelo candidato.
Questão 10
As sequências de números (a, -2, 1) e (2, b, 4) são inversamente proporcionais, então, o valor da soma a + b é igual a:
A) -1
B) 0
C) 1
D) 2
E) 4
Questão 11
(Enem) A resistência mecânica S de uma viga de madeira, em forma de um paralelepípedo retângulo, é diretamente proporcional à sua largura (b) e ao quadrado de sua altura (d) e inversamente proporcional ao quadrado da distância entre os suportes da viga, que coincide com o seu comprimento (x), conforme ilustra a figura. A constante de proporcionalidade k é chamada de resistência da viga.
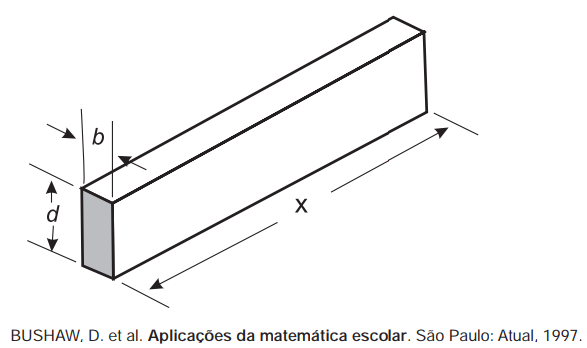
A expressão que traduz a resistência S dessa viga de madeira é:
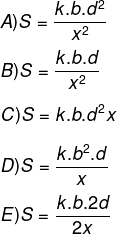
Questão 12
(IFSP) Para fazer uma viagem, levamos em consideração duas grandezas: velocidade do meio de transporte e tempo de viagem. Essas duas grandezas são:
A) completamente proporcionais.
B) desproporcionais.
C) diretamente proporcionais.
D) subitamente proporcionais.
E) inversamente proporcionais.
Resposta Questão 1
Alternativa E
Sabemos que essas grandezas se relacionam de forma inversamente proporcional, pois à medida que a velocidade aumentar, o tempo diminuirá. Então, temos que:
|
Velocidade |
Tempo |
|
60 km/h |
3 horas |
|
x |
2 horas |
Como as grandezas são inversamente proporcionais, temos que:
60 · 3 = 2x
180 = 2x
x = 180 : 2
x = 90 km/h
Resposta Questão 2
Alternativa B
Analisando as grandezas, sabemos que o volume é inversamente proporcional à densidade. Montando a tabela, é possível calcular o valor de x.
|
Densidade |
Volume |
|
80 g/cm³ |
x cm³ |
|
100 g/cm³ |
2 cm³ |
Então, multiplicando reto, temos que:
80x = 100 · 2
80x = 200
x = 200 : 80
x = 2,5 cm³
Resposta Questão 3
Resposta Questão 4
Alternativa B
Sejam x, y e z a produção dos funcionários de 28, 30 e 54 anos respectivamente, então, temos que:
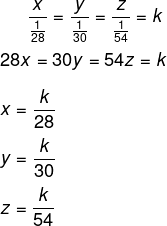
Realizando a soma x + y + z = 1324
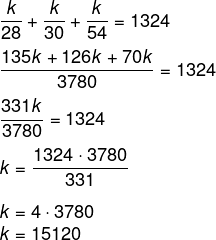
Conhecendo o valor de k, agora calcularemos a produção de cada um dos funcionários:
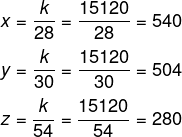
Podemos afirmar que o funcionário que possui 30 anos arquivou 504 processos.
Resposta Questão 5
Alternativa D
Sabemos que 6 operários levaram 18 dias para fazer a metade da obra, agora há 9 operários, então, podemos montar a tabela a seguir:
|
Operários |
Tempo |
|
6 |
18 |
|
9 |
x |
Multiplicando reto, temos que:
9x = 18 · 6
9x = 108
x = 108 : 8
x = 12
Sabemos que eles levarão 12 dias para finalizar a obra, logo, o tempo total gasto será: 18 + 12 = 30 dias.
Resposta Questão 6
Alternativa D
Sejam x, y e z os valores recebidos por cada um dos herdeiros, então, temos que:
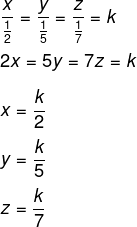
Sabemos que a soma x + y + z = 2.950.000.
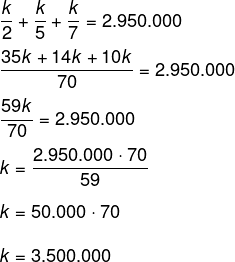
Agora queremos encontrar o valor recebido pelo herdeiro que teve a maior parte, então, temos que:
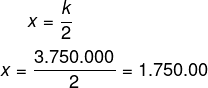
Resposta Questão 7
Alternativa B
Cada empresa receberá de forma inversamente proporcional ao tempo de uso da máquina, então, sejam x, y, z o recebimento de cada empresa, temos que:
![]()
Sabemos que a soma x + y + z = 31.000, logo, temos que:
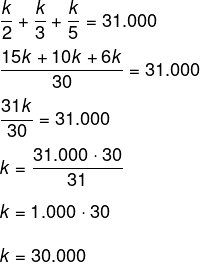
Conhecendo o valor de k, a empresa que tem maior idade é a de 5 anos, então, basta calcular k divido por 5.
![]()
Resposta Questão 8
Alternativa E
Sejam x, y e z a produção de cada uma das máquinas, temos que:
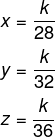
A soma de x + y + z = 3820, então, temos que:
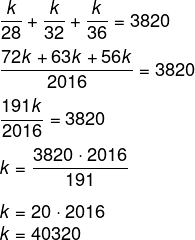
A máquina mais nova tem 28 meses de uso, então, basta realizar a divisão de k por 28.
![]()
Resposta Questão 9
Alternativa C
Sabemos que, quanto maior a vazão da água, menor o tempo que a mangueira levará para encher o reservatório.
Resposta Questão 10
Alternativa B
Sabendo que as grandezas são inversamente proporcionais, temos que:
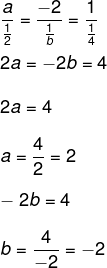
Assim, a soma a + b = 2 + (-2) = 0
Resposta Questão 11
Alternativa A
Multiplicamos a constante k pelos valores diretamente proporcionais e dividimos k pelos valores inversamente proporcionais, então, temos que b e d² são proporcionais a k, e x² é inversamente proporcional.
![]()
Resposta Questão 12
Alternativa E
Sabemos que à medida que a velocidade aumentar, o tempo diminuirá, o que faz com que essas grandezas sejam inversamente proporcionais.