Questão 1
Analisando o trapézio a seguir, podemos afirmar que a sua área é igual a:
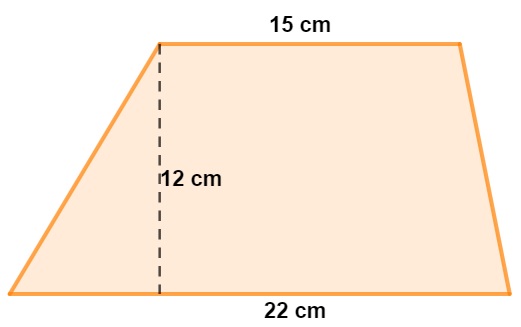
A) 444 cm²
B) 222 cm²
C) 148 cm²
D) 74 cm²
E) 60 cm
Questão 2
Um trapézio tem base maior medindo 12 centímetros, base menor igual a 8 centímetros e altura igual a 10 centímetros, então a área desse trapézio é igual a:
A) 75 cm²
B) 100 cm²
C) 110 cm²
D) 148 cm²
E) 204 cm²
Questão 3
Um trapézio tem área igual a 35 cm². O comprimento da sua base maior, sabendo que a sua altura é de 5 cm e a base menor mede 4 cm, é de:
A) 8 cm
B) 10 cm
C) 12 cm
D) 14 cm
E) 16 cm
Questão 4
Um terreno retangular teve sua área dividida em dois triângulos e um trapézio, como mostra a figura a seguir:
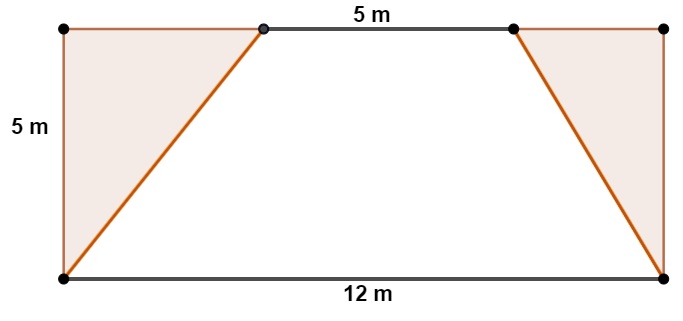
A soma da área dos dois triângulos em destaque é de:
A) 102,5 cm²
B) 60 cm²
C) 42,5 cm²
D) 35 cm²
E) 17,5 cm²
Questão 5
Qual é o comprimento da base maior de um trapézio que tem área igual a 50 cm², base menor igual a 4 cm e altura igual a 10 cm?
A) 3 cm
B) 4 cm
C) 5 cm
D) 6 cm
E) 8 cm
Questão 6
A área do trapézio isósceles com base maior igual a 30 cm, base menor igual a 25 cm e altura igual a 18 cm é igual a:
A) 495 cm²
B) 455 cm²
C) 349 cm²
D) 320 cm²
E) 300 cm²
Questão 7
A diferença entre a base maior e a base menor de um trapézio é de 6 cm. Sabendo que sua área é de 96 cm² e que sua altura é de 8 cm, então a base menor mede:
A) 6 cm
B) 7 cm
C) 8 cm
D) 9 cm
E) 10 cm
Questão 8
Um trapézio possui base maior igual a 13 cm e base menor igual a 5 cm. Sabendo que sua área é igual a 108 cm², então a altura desse trapézio é igual a:
A) 6
B) 8
C) 10
D) 12
E) 14
Questão 9
(Enem) O Esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.
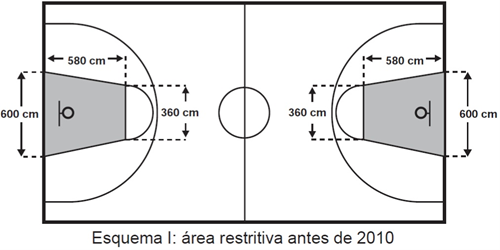
Visando a atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificaram as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
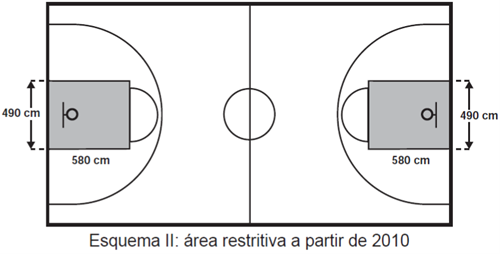
Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
A) aumento de 5800 cm².
B) aumento de 75.400 cm².
C) aumento de 214.600 cm².
D) diminuição de 63.800 cm².
E) diminuição de 272.600 cm².
Questão 10
Um terreno tem formato de trapézio com área de 195 m². Sabendo que sua base maior mede 16 metros e a menor mede 10 metros, então a largura desse terreno, em metros, é de:
A) 12 metros
B) 14 metros
C) 15 metros
D) 16 metros
E) 17 metros
Questão 11
Um trapézio tem base menor medindo 8 e base maior medindo o dobro da base menor. Sabendo que a sua altura é igual à média entre a base maior e a base menor, então a área desse trapézio é igual a:
A) 144 cm²
B) 196 cm²
C) 210 cm²
D) 224 cm²
E) 240 cm²
Questão 12
Sobre o trapézio, julgue as afirmativas a seguir:
I- É um polígono de 4 lados.
II- Sua área é igual à soma das suas bases dividido por 2.
III- É um quadrilátero, porém não é um paralelogramo.
Marque a alternativa correta:
A) Somente a I é falsa.
B) Somente a II é falsa.
C) Somente a III é falsa.
D) Todas são verdadeiras.
Resposta Questão 1
Alternativa B
Dados:
- B = 22
- h = 12
- b = 15
Calculando a área, temos que:
\(A=\frac{\left(B+b\right). h}{2}\)
\(A=\frac{\left(22+15\right)\cdot12}{2}\)
\(A=\frac{37\cdot12}{2}\)
\(A\ =\ 37\ \cdot6\ \)
\(A\ =\ 222\ cm²\)
Resposta Questão 2
Alternativa C
Dados:
- B = 12
- b = 8
- h = 10
\(A=\frac{\left(B+b\right)·h}{2}\)
\(A=\frac{\left(12+8\right)\cdot10}{2}\)
\(A=\frac{22\cdot10}{2}\)
\(A\ =\ 11\ \cdot10\ \)
\(A\ =\ 110\ cm²\)
Resposta Questão 3
Alternativa B
Dado que A = 35, h = 5 e b = 4, então temos que:
\(A=\frac{\left(B+b\right)·h}{2}\)
\(35=\frac{\left(B+4\right)\cdot5}{2}\)
\(35\cdot2=\left(B+4\right)\cdot5\)
\(70\ =\ 5B\ +\ 20\)
\(70\ – 20 = 5B\)
\(50\ =\ 5B\ \)
\(B=\frac{50}{5}\)
\(B=10\ cm\)
Resposta Questão 4
Alternativa E
A área em destaque é igual à diferença entre a área do retângulo e a área do trapézio.
O retângulo tem dimensões 12 m e 5 m, então sua área será igual a:
\(A=b·h=12\cdot5=60\ cm²\)
Agora, calculando a área do trapézio, temos que:
- h = 5
- B = 12
- b = 5
\(A=\frac{\left(B+b\right)·h}{2}=\frac{\left(12+5\right)\cdot5}{2}=\frac{17\cdot5}{2}=\frac{85}{2}=42,5\ \ cm^2\)
Então a diferença entre as áreas é de:
\(60 – 42,5 = 17,5\)
Resposta Questão 5
Alternativa D
Dados:
- A = 50
- b = 4
- h = 10
\(A=\frac{\left(B+b\right)·h}{2}\)
\(50=\frac{\left(B+4\right)\cdot10}{2}\)
\(50\cdot2\ =\ 10B\ +\ 40\ \)
\(100=10B+40\ \)
\(100-40=10B\)
\(60=10B\)
\(B=\frac{60}{10}\)
\(B=6\)
Resposta Questão 6
Alternativa A
Calculando a área do trapézio, temos que:
- B = 30
- b = 25
- h = 18
\(A=\frac{\left(B+b\right)·h}{2}\)
\(A=\frac{\left(30+25\right)\cdot18}{2}\)
\(A=\frac{55\cdot18}{2}\)
\(A\ =\ 55\ \cdot9\ \)
\(A=495\ cm²\)
Resposta Questão 7
Alternativa D
Sabemos que:
\(B – b = 6 \)
\(B = 6 + b\)
Dados:
- h = 8 cm
- A = 96 cm²
Temos que:
\(A=\frac{\left(B+b\right)·h}{2}\)
\(96=\frac{\left(6+b+b\right)\cdot8}{2}\)
\(96=\left(6+2b\right)\cdot4\)
\(\frac{96}{4}=6+2b\)
\(24=6+2b\ \)
\(24-6=2b\)
\(18=2b\)
\(b=\frac{18}{2}\)
\(b=9\ \)
Resposta Questão 8
Alternativa D
Dados:
- B = 13
- b = 5
- A = 108
\(A=\frac{\left(B+b\right)·h}{2}\)
\(108=\frac{\left(13+5\right)·h}{2}\)
\(108=\frac{18h}{2}\)
\(108=9h\)
\(h=\frac{108}{9}\)
\(h=12\ cm\)
Resposta Questão 9
Alternativa A
Primeiro calcularemos a área do trapézio dos garrafões no Esquema I.
\(A=\frac{\left(B+b\right)·h}{2}\)
\(A=\frac{\left(600+380\right)\cdot580}{2}\)
\(A=\frac{980\cdot580}{2}\)
\(A=\frac{556800}{2}\)
\(A=278400\)
Agora calcularemos a área do retângulo dos garrafões no Esquema II.
\(A=b·h\)
\(A=580\cdot490\)
\(A=284.200\)
Note que, no Esquema II, o garrafão é maior, logo, houve um aumento:
\(284.200 – 278.400 = 5800 cm²\)
Resposta Questão 10
Alternativa C
Nesse caso, a largura do terreno é igual à altura do trapézio, logo, temos que:
- B = 16
- b = 10
- A = 195
\(A=\frac{\left(B+b\right)·h}{2}\)
\(195=\frac{\left(16+10\right)·h}{2}\)
\(195=\frac{26h}{2}\)
\(195=13h\)
\(h=\frac{195}{13}\)
\(h=15\)
Resposta Questão 11
Alternativa A
Se a base menor mede 8, então a base maior mede 16, pois ela é o dobro da base menor.
Calculando a altura, como ela é a média entre 8 e 16, então temos que:
\(h = (8 + 16) : 2 = 24 : 2 = 12\)
Assim, calculando a área, temos que:
\(A=\frac{\left(16+8\right)\cdot12}{2}\)
\(A=24\cdot6\)
\(A=144\ cm^2\)
Resposta Questão 12
I- Ele é um polígono de 4 lados. (verdadeira)
O trapézio de fato satisfaz as definições de polígono e possui 4 lados.
II- Sua área é igual à soma das suas bases dividido por 2. (falsa)
A área do trapézio é igual à soma das duas bases vezes a altura dividido por 2.
III- O trapézio não é um paralelogramo. (verdadeira)
O trapézio possui 2 lados paralelos e 2 não paralelos, logo, ele não é um paralelogramo.



