Questão 1
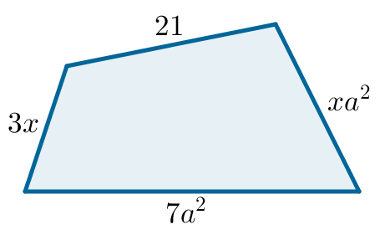
Qual é a forma fatorada da expressão algébrica que representa o perímetro da figura a seguir?
a) (3 + a2)(x + 7)
b) (3 + 7)(x + a2)
c) 7(3 + a2)
d) a2(x + 7)
e) a2 + x
Questão 2
Qual o resultado mais simplificado da divisão da expressão 4ky – 6y + 2kz – 3z pela expressão 2k – 3?
a) (2y + z)(2k + z)
b) 2y + z
c) (2y + z)(2k + 3)
d) 2k + 3
e) 4k + 6
Questão 3
Um dos fatores da forma fatorada mais reduzida do polinômio 4x2 + 6x4 – 8x5 + 6x3 é:
a) x
b) 2x
c) 3x
d) 2x2
e) 2x4
Questão 4
Qual é a forma fatorada mais reduzida do polinômio 4x2y3z4 – 16x3y2?
a) 4x2y2
b) yz4 – 4x
c) 4x2y2(yz4 – 4x)
d) 4x2y2z3(yz – 4x)
e) x2y2(4yz4 – 16x)
Resposta Questão 1
O perímetro de um polígono é determinado pela soma das medidas de seus lados, logo:
3x + 21 + 7a2 + xa2
Colocando os fatores semelhantes dos dois primeiros termos em evidência, teremos:
3x + 3·7 + 7a2 + xa2
3(x + 7) + 7a2 + xa2
Colocando os fatores semelhantes dos dois últimos termos em evidência e mudando a ordem da soma obtida, teremos:
3(x + 7) + 7a2 + xa2
3(x + 7) + a2(7 + x)
3(x + 7) + a2(x + 7)
Colocando o fator x + 7 em evidência, teremos:
3(x + 7) + a2(x + 7)
(3 + a2)(x + 7)
Alternativa A
Resposta Questão 2
Para resolver esse problema, escreva a divisão na forma de fração e fatore o numerador:
4ky – 6y + 2kz – 3z
2k – 3
2·2ky – 2·3y + 2kz – 3z
2k – 3
2y(2k – 3) + z(2k – 3)
2k – 3
(2y + z)(2k – 3)
2k – 3
2y + z
Alternativa B
Resposta Questão 3
O polinômio do exercício pode ser reescrito da seguinte maneira:
4x2 + 6x4 – 8x5 + 6x3
2·2x2 + 2·3x2x2 – 2·4x3x2 + 2·3xx2
Note que os fatores em comum em todos os termos são 2 e x2. Colocando-os em evidência, teremos:
2·2x2 + 2·3x2x2 – 2·4x3x2 + 2·3xx2
2x2(2 + 2x2 – 4x3 + 3x)
Alternativa D
Resposta Questão 4
Colocando os fatores comuns em evidência, teremos:
4x2y3z4 – 16x3y2
4x2y2(yz4 – 4x)
Alternativa C