Questão 1
Um joão-de-barro voa de seu ninho até um lago, que fica a 100 m de distância, a fim de conseguir barro para finalizar a sua casa. Supondo que o pássaro manteve uma velocidade constante em todo o trajeto de 36 km/h e que, na volta ao ninho, enfrentou um vento contrário de 2 m/s, determine o tempo total que foi gasto para que o pequeno animal fizesse o trajeto completo. Desconsidere o tempo gasto pelo joão-de-barro para conseguir o barro.
a) 30 s
b) 20,2 s
c) 15 s
d) 25,4 s
e) 22,5 s
Questão 2
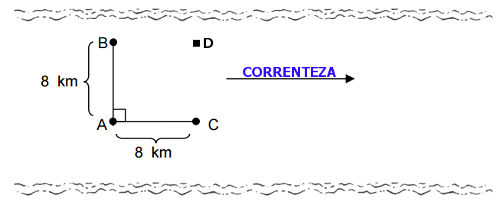
A correnteza de um rio possui velocidade de 4m/s no sentido indicado na figura abaixo. Um nadador percorrerá a diagonal AD do quadrado ABCD em razão da composição de seu movimento com o movimento da correnteza e, para isso, ele deve manter uma velocidade constante de 3 m/s no sentido AB. Sendo assim, determine o valor aproximado do tempo que será gasto pelo nadador no percurso AD.
DADOS: √2 = 1,4
a) 37,7 min
b) 42,8 min
c) 30 min
d) 35,5 min
e) 40 min
Questão 3
(UFMS) Um carro move-se com velocidade constante de 60 km/h. Começa a chover e o motorista observa que as gotas de água da chuva caem formando um ângulo de 30° com a vertical. Considerando que, em relação à Terra, as gotas caem verticalmente, qual a velocidade em que as gotas de água caem em relação ao carro?
a) 30√3 km/h.
b) 60 km/h.
c) 120 km/h.
d) 30 km/h.
e) 80km/h.
Questão 4
(PUC) Um avião em voo horizontal voa a favor do vento com velocidade de 180 Km/h em relação ao solo. Na volta, ao voar contra o vento, o avião voa com velocidade de 150 Km/h em relação ao solo. Sabendo-se que o vento e o módulo da velocidade do avião (em relação ao ar) permanecem constantes, o módulo da velocidade do avião e do vento durante o voo, respectivamente, são:
a) 165 Km/h e 15 Km/h
b) 160 Km/h e 20 Km/h
c) 155 Km/h e 25 Km/h
d) 150 Km/h e 30 Km/h
e) 145 Km/h e 35 Km/h
Questão 5
(IFBA) Dois veículos A e B trafegam numa rodovia plana e horizontal, obedecendo as seguintes equações horárias, cujas unidades estão expressas no Sistema internacional de medidas (S.I.):
XA = 200,0 + 10,0t e XB = 1000,0 – 30,0t
Ao analisar esses movimentos, pode-se afirmar que a velocidade relativa de afastamento dos veículos, em km/h, vale:
a) 20,0
b) 40,0
c) 80,0
d) 100,0
e) 144,0
Questão 6
(Unitau) Uma motocicleta com velocidade constante de 20 m/s ultrapassa um trem de comprimento 100 m e velocidade 15 m/s. A duração da ultrapassagem é:
a) 5 s
b) 15 s
c) 20 s
d) 25 s
e) 30 s
Questão 7
Dois móveis movimentam-se de acordo com as seguintes funções horárias:
SA = 15 + 25.t
SB = 20 + 30.t
Marque a alternativa correta a respeito do movimento desses objetos:
a) A velocidade relativa de aproximação dos móveis é de 5 m/s.
b) Não há movimento relativo de aproximação ou afastamento dos móveis.
c) O móvel A afasta-se de B com uma velocidade de 5 m/s
d) O móvel B afasta-se de A com uma velocidade de 5 m/s.
e) O movimento do móvel A é classificado como retrógrado.
Questão 8
Um ônibus e uma moto movimentam-se, no mesmo sentido, com velocidades de 20 m/s e 30 m/s, respectivamente. Sentado a uma das janelas do ônibus, um passageiro marca um tempo de 3 s para que a moto ultrapasse o ônibus. Determine o tamanho do ônibus.
a) 30 m
b) 25 m
c) 15 m
d) 10 m
e) 12 m
Resposta Questão 1
Letra E
Determinaremos o tempo gasto pelo pássaro na ida e na volta.
⇒ Ida: Dividindo a velocidade 36 km/h por 3,6 para transformar a unidade de km/h para m/s, encontraremos 10 m/s, logo:
VM = Δs
ΔtIDA
10 = 100
ΔtIDA
ΔtIDA = 10 s
⇒ Volta: Como o pássaro enfrenta vento contrário de 2 m/s, sua velocidade no percurso cai para 8 m/s, portanto:
VM = Δs
ΔtVOLTA
8 = 100
ΔtVOLTA
ΔtVOLTA = 12,5 s
Logo, o tempo toral é: T = ΔtIDA + ΔtVOLTA = 10 + 12,5 = 22,5 s
Resposta Questão 2
Letra A
O nadador percorrerá a diagonal AD por causa da composição de sua velocidade com a velocidade da correnteza. Sabendo que o ângulo entre os percursos AB e AC é de 90°, temos:
Distância resultante AD:
DAD2 = DAB2 + DAC2
DAD2 = 82 + 82
DAD2 = 64+64
DAD2 = 128
DAD = √128
DAD ≈11,3 km = 11300 m
Velocidade resultante entre AD:
VAD2 = VNADADOR2 + VCORRENTEZA2
VAD2 = 32 + 42
VAD2 = 9 + 16
VAD = √25
VAD = 5 m/s
Fazendo a velocidade média para o trecho AD, temos:
VAD = DAD → 5 = 11300 → Δt = 2260 s ≈ 37,7 min
Δt Δt
Resposta Questão 3
Letra C
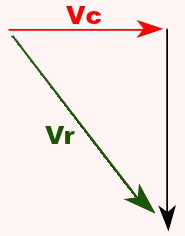
A imagem mostra Vc como a velocidade do carro e Vr como a velocidade resultante da chuva em relação ao carro. O ângulo formado entre Vr e a reta na vertical é de 30°, portanto:
sen 30° = Vc
Vr
0,5 = 60
Vr
Vr = 120 km/h
Resposta Questão 4
Letra A
Partindo das informações do enunciado e tendo Vv como a velocidade do vento e Va como a velocidade do avião, podemos entender que, voando a favor do vento, a velocidade da aeronave deve ser somada à do vento e, no voo contra o vento, deve haver uma subtração de velocidades. Logo, podemos montar um sistema:
Va + Vv = 180
Va – Vv = 150
No sistema acima, podemos somar termo a termo, de modo que Va + Va = 2Va; +Vv – Vv = 0 e 180 + 150 = 330
Portanto:
2.Va = 330
Va = 165 km/h
Logo, Vv = 180 – Va = 180 – 165 = 15 km/h
Resposta Questão 5
Letra E
A função horária utilizada foi: S = S0 + v.t, portanto, os valores 10 e – 30 correspondem, respectivamente, às velocidades dos objetos A e B em m/s. O sinal negativo da velocidade do móvel B indica que seu sentido de movimento é oposto ao do móvel A. Se ocorre afastamento entre os objetos, podemos entender que um se movimenta para a direita, enquanto o outro movimenta-se para a esquerda, de modo a afastarem-se. Nesse caso, a velocidade relativa será determinada pela soma dos módulos das velocidades de cada móvel:
VREL = 30 + 10 = 40 m/s x 3,6 = 144 km/h
Resposta Questão 6
Letra C
O movimento dos móveis ocorre no mesmo sentido, logo, pode-se determinar a velocidade relativa da moto em relação ao trem como sendo a subtração entre os módulos das velocidades dos dois veículos:
VREL = 20 – 15 = 5 m/s
Podemos concluir que a moto movimenta-se a 5 m/s em relação ao trem. Por meio da definição de velocidade média, e sabendo que o trem possui 100 m de comprimento, temos:
V = Δs ÷ Δt
5 = 100 ÷ Δt
5. Δt = 100
Δt = 100 ÷ 5
Δt = 20 s.
Resposta Questão 7
Letra D
A função horária utilizada foi: S = S0 + v.t, portanto, os valores 25 e 30 correspondem, respectivamente, às velocidades dos objetos A e B em m/s. As velocidades possuem o mesmo sinal, logo o movimento dos móveis ocorre no mesmo sentido, e a velocidade relativa entre os móveis será dada pela subtração das velocidades de cada um:
VREL = 30 – 25 = 5 m/s
O corpo B afasta-se de A com uma velocidade de 5 m/s.
Resposta Questão 8
Letra A
Como o movimento dos móveis ocorre no mesmo sentido e a velocidade da moto é maior, podemos concluir que a velocidade relativa de aproximação será dada pela subtração das velocidades dos móveis.
VREL = 30 – 20 = 10 m/s
Pode-se concluir que a moto tem uma velocidade de 10 m/s em relação ao ônibus. Por meio da definição de velocidade média, podemos determinar o tamanho do ônibus:
V = Δs ÷ Δt
10 = Δs ÷ 3
Δs = 3 . 10 = 30 m



