Questão 1
Dadas uma circunferência C e um círculo A, ambos de centro O e de raio r, assinale a alternativa correta:
a) Se um ponto P é escolhido, de modo que a distância entre P e O é menor que r, então, o ponto P pertence ao círculo e à circunferência.
b) Se um ponto P é escolhido, de modo que a distância entre P e O é igual a r, então, o ponto P pertence somente à circunferência.
c) Se um ponto P é escolhido, de modo que a distância entre P e O é igual a r, então, o ponto P pertence ao círculo e à circunferência.
d) Se um ponto P é escolhido, de modo que a distância entre P e O é maior que r, então P pertence ao círculo, mas não à circunferência.
e) NDA.
Questão 2
Cordas e diâmetros são elementos das circunferências. Isso significa que a existência desses elementos depende da existência dessa figura. A respeito desses elementos, assinale a alternativa correta:
a) Cordas e diâmetros são elementos totalmente independentes, ou seja, não têm nada em comum.
b) Como o diâmetro é igual a duas vezes o raio e as cordas não, não podemos afirmar que diâmetro e cordas têm alguma relação.
c) Como o diâmetro é o dobro do raio, os lados AO e OB do triângulo AOB formam um diâmetro desde que sejam raios de uma circunferência.
d) Um diâmetro é uma corda que passa pelo centro da circunferência.
e) Um raio é uma corda que vai até o centro da circunferência.
Questão 3
Um ciclista deu 30 voltas em uma pista com formato de circunferência. Ao olhar seus equipamentos de medida, ele percebeu que a distância percorrida nessas 30 voltas foi de 90 km. Qual a medida aproximada do raio da pista em que se encontrava? (Considere π = 3,14).
a) 0,48 km.
b) 0,58 km.
c) 0,68 km.
d) 0,78 km.
e) 0,88 km.
Questão 4
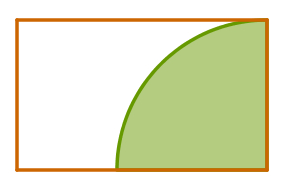
Um terreno tem formato retangular e seu dono resolveu colocar grama no setor circular cujo raio é igual a uma das laterais do terreno, conforme mostra a imagem. Sabendo que o perímetro do terreno é de 80 metros e que o lado menor é igual a 60% do lado maior, qual é a área do terreno que receberá grama?
a) 25 m2
b) 15 m2
c) 173,6 m2
d) 179,6 m2
e) 176,6 m2
Resposta Questão 1
Para resolver essa questão, note que o círculo e a circunferência “são coincidentes”, pois possuem o mesmo raio e centro.
a) Incorreta!
Quando a distância entre P e O é menor que r, o ponto P pertence ao círculo, mas não pertence à circunferência.
b) Incorreta!
Quando a distância entre P e O é igual a r, então, o ponto P pertence tanto à circunferência quanto ao círculo.
c) Correta!
d) Incorreta!
Quando a distância entre P e O é maior que r, então, o ponto P não pertence nem ao círculo nem à circunferência.
e) Incorreta, pois a alternativa c está correta.
Gabarito: Letra C.
Resposta Questão 2
Um diâmetro é uma corda que passa pelo centro da circunferência. Diante disso, a alternativa correta é a letra D. Entretanto, é importante comentar as alternativas B, C e E, já que a alternativa A é apenas a negação da correta.
Alternativa B: O diâmetro realmente é o dobro do raio, mas a definição do diâmetro relaciona-o com as cordas.
Alternativa C: Um triângulo é formado por três pontos não lineares. Isso significa que dois lados de um triângulo jamais poderão ser uma corda, pois a corda é um único segmento de reta.
Alternativa E: Uma corda é um segmento de reta que liga dois pontos de uma circunferência. Como o centro não é um ponto de uma circunferência, então, o raio não pode ser uma corda.
Gabarito: Letra D.
Resposta Questão 3
Por meio da expressão usada para encontrar o comprimento da circunferência, é possível determinar seu raio. O comprimento dessa circunferência é:
90 = 3 km
30
Substituindo os valores na expressão usada para encontrar o comprimento da circunferência, temos:
C = 2πr
3 = 2·3,14·r
3 = 6,28r
6,28r = 3
r = 3
6,28
r = 0,48 km, aproximadamente.
Gabarito: Letra A.
Resposta Questão 4
Primeiro, será necessário descobrir as dimensões do retângulo e, depois, calcular a área do setor circular. O lado maior mede x e o menor mede 60% de x. Fazendo os cálculos para encontrar o perímetro, temos:
x + 60% de x + x + 60% de x = 80
2x + 60x + 60x = 80
100 100
2x + 120x = 80
100
2x + 1,2x = 80
3,2x = 80
x = 80
3,2
x = 25 metros
O lado menor mede 60% de x, ou seja:
60·25 = 1500 = 15 metros
100 100
O lado menor é o raio do setor circular. O ângulo dessa figura é também um dos ângulos internos do retângulo: 90°. Assim, a área do setor circular de 90° é dada por:
A = 90πr2
360
A = 90·3,14·152
360
A = 282,6·225
360
A = 36585
360
A = 176,6 m2 de grama, aproximadamente.
Gabarito: Letra E.