Questão 1
Qual é a média ponderada dos números 1, 2, 3, 4, 5, 6, 7, 8 e 9, sabendo que seus respectivos pesos são 5, 5, 5, 5, 4, 4, 4, 4, 2?
a) 4,5
b) 2,8
c) 4,2
d) 2,9
e) 4,4
Questão 2
Uma empresa de comunicação conta com duas categorias de funcionários: Telemarketing e diretoria. Os funcionários da primeira categoria recebem R$ 950,00 mensalmente, enquanto os da segunda recebem R$ 9500,00. Sabendo que essa empresa possui 63 funcionários no setor de telemarketing e 5 diretores, o salário médio pago a eles é de, aproximadamente:
a) R$ 5985,00
b) R$ 4750,00
c) R$ 1580,00
d) R$ 950,00
e) R$ 9500
Questão 3
(UNCISAL/2015) Em cada bimestre, uma faculdade exige a realização de quatro tipos de avaliação, calculando a nota bimestral pela média ponderada dessas avaliações. Se a tabela apresenta as notas obtidas por uma aluna nos quatro tipos de avaliações realizadas e os pesos dessas avaliações,
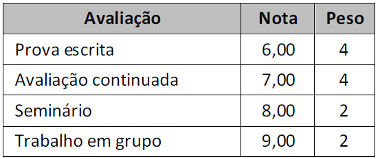
sua nota bimestral foi aproximadamente igual a
a) 8,6.
b) 8,0.
c) 7,5.
d) 7,2.
e) 6,8.
Questão 4
(UNIUBE MG/2014) Um aluno deve atingir 70 pontos para ser aprovado. Esse total de pontos é resultado de uma média ponderada de 3 notas, N1, N2 e N3, cujos pesos são, respectivamente, 1, 2, 2.
As suas notas, N1 e N2, são, respectivamente, em um total de 100 pontos distribuídos em cada uma, 50 e 65. Para ser aprovado, a sua nota N3 (em 100 pontos distribuídos) deverá ser:
a) Maior ou igual a 70 pontos.
b) Maior que 70 pontos.
c) Maior que 85 pontos.
d) Maior ou igual a 85 pontos.
e) Maior ou igual a 80 pontos.
Resposta Questão 1
Para calcular a média ponderada, basta dividir a soma dos produtos dos números pelo respectivo peso pela soma dos pesos:
M = 1·5 + 2·5 + 3·5 + 4·5 + 5·4 + 6·4 + 7·4 + 8·4 + 9·2
5 + 5 + 5 + 5 + 4 + 4 + 4 + 4 + 2
M = 5 + 10 + 15 + 20 + 20 + 24 + 28 + 32 + 18
38
M = 172
38
M = 4,5
Gabarito: Letra A.
Resposta Questão 2
Essa questão, na realidade, deveria ser resolvida com média aritmética. Contudo, para descartar a necessidade de somar 63 parcelas de 950, podemos usar multiplicação ou nos valermos do conceito de média ponderada:
M = 63·950 + 5·9500
63 + 5
M = 59850 + 47500
68
M = 107350
68
M = 1578,68
Gabarito: Letra C.
Resposta Questão 3
Lembre-se de que a média ponderada é calculada somando-se os produtos entre pesos e notas e dividindo-se o resultado pela soma dos pesos. Portanto:
M = 6·4 + 7·4 + 8·2 + 9·2
4 + 4 + 2 + 2
M = 24 + 28 + 16 + 18
12
M = 86
12
M = 7,17
Gabarito: Letra D.
Resposta Questão 4
Lembre-se de que a média ponderada é a soma dos produtos dos respectivos pesos pelas notas dividida pela soma dos pesos. Portanto:
70 = 1·50 + 2·65 + 2·x
5
70 = 50 + 130 + 2·x
5
5·70 = 50 + 130 + 2·x
350 = 50 + 130 + 2·x
350 – 50 – 130 = 2·x
350 – 180 = 2·x
170 = 2x
x = 170
2
x = 85
A nota que o aluno deve tirar é 85, portanto maior ou igual a 85
Gabarito: Letra D.



