Questão 2
Analise a equação a seguir:
\(2^{x^2-4}=128\)
Sobre essa equação, podemos afirmar que:
A) É uma equação polinomial do 1º grau.
B) É uma equação polinomial do 2º grau.
C) É uma equação trigonométrica.
D) É uma equação exponencial.
E) É uma equação logarítmica.
Questão 3
Encontre o valor de x na equação:
\(3^{x+2}+3^x=2430\)
A) x = 5
B) x = 4
C) x = 3
D) x = 2
E) x = 1
Questão 4
O conjunto de soluções da equação exponencial \(3\cdot2^{x^2-4}=48\) é:
\(A) x = \pm2\)
\(B) x = \pm2\sqrt2\)
\(C) x = \pm4 \)
\(D) x = \pm4\sqrt2\)
\(E) x = \pm\sqrt6\)
Questão 5
O montante de determinado capital em um fundo de investimento, após o tempo t em anos, é dado pela fórmula \(M\left(t\right)=C\cdot{1,5}^t\) . Nessas condições, o tempo necessário para que um capital de R$ 800 investido gere um montante de R$ 4050 é de:
A) 3 anos
B) 4 anos
C) 5 anos
D) 6 anos
E) 7 anos
Questão 6
A quantidade de bactérias de uma cultura, depois de t horas, é dada pela expressão \(Q\left(t\right)=Q_0\cdot2^t\) , em que Q0 é a quantidade inicial de bactérias. Nessas condições, se inicialmente havia 1500 bactérias, após quantas horas haverá 12.000 bactérias?
A) 1 hora
B) 3 horas
C) 5 horas
D) 7 horas
E) 8 horas
Questão 7
Durante um experimento, obteve-se a fórmula para a população de bactérias:
\(q\left(t\right)=20\cdot2^{3t}\)
Em que t é o tempo, em hora, e q(t) é a população, em milhares de bactérias. Se a população de bactérias era incialmente de 20 mil, então após quanto tempo ela será dobrada?
A) 3 horas
B) 1 hora
C) 30 minutos
D) 20 minutos
E) 10 minutos
Questão 8
Sabendo que \(x = \left(\frac{1}{5}\right)^{\left(2t+1\right)} \) e \(y=\left(0,2\right)^{3t\ -\ 2\ }\), o valor de y que faz com que x seja igual a y é:
A) -1
B) 0
C) 1
D) 2
E) 3
Questão 9
Dada a equação exponencial \(3^{x^2-x}=9\) , a soma das soluções dessa equação é:
A) -1
B) 0
C) 1
D) 2
E) 3
Questão 10
(Enem 2020) Enquanto um ser está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ele morre, essa quantidade vai diminuindo. Sabe-se que a meia-vida do carbono 14 é de 5730 anos, ou seja, num fóssil de um organismo que morreu há 5730 anos, haverá metade do carbono 14 que existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado: \(Q\left(t\right)=Q_0\cdot2^\frac{-t}{5730}\) , em que t é o tempo, medido em anos, Q(t) é a quantidade de carbono 14 no ser vivo correspondente.
Um grupo de arqueólogos, numa de suas expedições, encontrou 5 fósseis de espécies conhecidas e mediram a quantidade de carbono 14 neles existente. Na tabela, temos esses valores juntamente à quantidade de carbono 14 nas referidas espécies vivas.
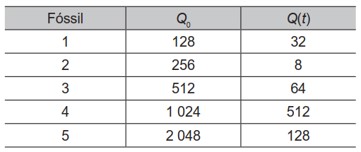
O fóssil mais antigo encontrado nessa expedição foi:
A) 1
B) 2
C) 3
D) 4
E) 5
Questão 11
Utilizamos a potenciação para modelar fenômenos que crescem muito rápido, por exemplo, o crescimento das infecções de um vírus durante uma pandemia. Suponha que o número de infectados se inicia em 2 e que cada pessoa infectada infecte outras 3, ou seja, na primeira semana, haverá 6 infectadas, na segunda, 18, e assim sucessivamente. Supondo que o ritmo de infecção continue o mesmo por, pelo menos, um ano, então, após quantas semanas, haverá 4374 pessoas infectadas?
A) 5 semanas
B) 6 semanas
C) 7 semanas
D) 8 semanas
E) 9 semanas
Questão 12
Quando uma matéria é radioativa, é comum que a sua massa se desintegre ao decorrer do tempo de forma exponencial. O césio 137, por exemplo, possui meia-vida após 30 anos, ou seja, se havia inicialmente uma massa m0 de césio, após 30 anos, haverá metade de m0. Então, para descrever melhor essa situação, temos a função exponencial:
\(f\left(x\right)=\frac{m_0}{2^x}\)
- x→ quantidade de meias-vidas
- m0 → massa inicial
- f(x) → massa final
Pensando nisso, se houver 80 gramas de césio 137 inicialmente, após quanto tempo haverá somente 2,5 gramas dele?
A) 150 anos
B) 120 anos
C) 100 anos
D) 80 anos
E) 50 anos
Resposta Questão 1
Alternativa C
Sabemos que 32 = 25, logo, temos que:
\(2^{x+1}=2^5\)
Igualando os expoentes, temos que:
\(x+1=5\)
\(x=5-1\)
\(x=4\)
Resposta Questão 2
Alternativa D
A equação é exponencial, pois há incógnita no expoente.
Resposta Questão 3
Alternativa A
Sabemos que:
\(3^{x+2}+3^x=2430\)
\(3^x\cdot3²+3x=2430\)
\(3^x3²+1=2430\)
\(3^x\cdot\left(9+1\right)=2430\)
\(3^x\cdot10=2430\)
\(3^x=\frac{2430}{10}\)
\(3^x=243\)
\(3^x=3^5\)
\(x=5\ \)
Resposta Questão 4
Alternativa B
\(3\cdot2^{x^2-4}=48\)
\(2^{x^2-4}=\frac{48}{3}\)
\(2^{x^2-4}=16\)
\(2^{x^2-4}=2^4\)
\(x^2-4=4\)
\(x^2=8\)
\(x=\pm\sqrt8\)
\(x=\pm\sqrt{4\cdot2}\)
\(x=\pm2\sqrt2\)
Resposta Questão 5
Alternativa C
Sabemos que C = 800 e M(t) = 4050, logo, temos que:
\(4050=800\cdot{1,5}^t\)
\(\frac{4050}{800}={1,5}^t\)
\(5,0625={1,5}^t\)
\({1,5}^5={1,5}^t\)
\(t=5\ \)
O tempo é de 5 anos.
Resposta Questão 6
Alternativa B
Substituindo Qt = 12.000 e Q0 = 1500 , temos que:
\(12.000=1500\cdot2^t\)
\(\frac{12.000}{1500}=2^t\)
\(8=2^t\)
\(2^3=2^t\)
\(t=3\ \)
O tempo gasto foi de 3 horas.
Resposta Questão 7
Alternativa D
Substituindo q(t) = 40, temos que:
\(40=20\cdot2^{3t}\)
\(\frac{40}{20}=2^{3t}\)
\(2=2^{3t}\)
\(1=3t\)
\(t=\frac{1}{3}\)
Como o t é o tempo em horas, e um terço de 1 hora é igual a 60 minutos, dividindo por 3, temos:
60 : 3 = 20 minutos
Resposta Questão 8
Alternativa E
Sabemos que 0,2 = 15 , então temos que:
\(\left(\frac{1}{5}\right)^{\left(2t+1\right)}=\left(0,2\right)^{3t\ -\ 2\ }\)
\(\left(\frac{1}{5}\right)^{\left(2t+1\right)}=\left(\frac{1}{5}\right)^{3t\ -\ 2\ }\)
\(2t+1=3t-2\ \)
\(2t-3t=-\ 2-1\ \)
\(-t=-3\ \)
\(t=3\)
Resposta Questão 9
Alternativa C
Sabemos que:
\(3^{x^2-x}=3^2\)
\(x^2-x=2\)
\(x^2-x-2=0\)
Resolvendo a equação do 2º grau calculando o delta, temos que:
- a = 1
- b = -1
- c = -2
\(\Delta=b^2-4ac\)
\(\Delta=\left(-1\right)^2-4\cdot1\cdot\left(-2\right)\)
\(\Delta=1+8\)
\(\Delta=9\ \)
Agora calculando as raízes da equação:
\(x=\frac{-b\pm\sqrt\Delta}{2a}\)
\(x=\frac{-\left(-1\right)\pm\sqrt9}{2\cdot1}\)
\(x=\frac{1\pm3}{2}\)
\(x_1=\frac{1+3}{2}=\frac{4}{2}=2\)
\(x_2=\frac{1-3}{2}=\frac{-2}{2}=-1\)
Então a soma das soluções é: 2 + (-1) = 1
Resposta Questão 10
Alternativa B
Calcularemos o valor de t para cada um dos fósseis substituindo os valores dados na tabela.
- Fóssil 1
\(Q\left(t\right)=Q_0\cdot2^\frac{-t}{5730}\ \)
\(32=128\cdot2^\frac{-t}{5730}\)
\(\frac{32}{128}=2^\frac{-t}{5730}\)
\(\frac{1}{4}=2^\frac{-t}{5730}\)
\(2^{-2}=2^\frac{-t}{5730}\)
\(-\ 2=\frac{-t}{5730}\)
\(2=\frac{t}{5730}\)
\(t=2\cdot5730\)
- Fóssil 2
\(8=256\cdot2^\frac{-t}{5730}\)
\(\frac{8}{256}=2^\frac{-t}{5730}\)
\(\frac{1}{32}=2^\frac{-t}{5730}\)
\(2^{-5}=2^\frac{-t}{5730}\)
\(-5=\frac{-t}{5730}\)
\(t=5\cdot5730\)
- Fóssil 3
\(64=512\cdot2^\frac{-t}{5730}\)
\(\frac{64}{512}=2^\frac{-t}{5730}\)
\(\frac{1}{8}=2^\frac{-t}{5730}\)
\(2^{-3}=2^\frac{-t}{5730}\)
\(-3=\frac{-t}{5730}\)
\(t=3\cdot5730\ \)
- Fóssil 4
\(512=1024\cdot2^\frac{-t}{5730}\)
\(\frac{512}{1024}=2^\frac{-t}{5730}\)
\(\frac{1}{2}=2^\frac{-t}{5730}\)
\(2^{-1}=2^\frac{-t}{5730}\)
\(-1=\frac{-t}{5730}\)
\(t=5730\cdot1\ \)
- Fóssil 5
\(128=2048\cdot2^\frac{-t}{5730}\)
\(\frac{128}{2048}=2^\frac{-t}{5730}\)
\(\frac{1}{16}=2^\frac{-t}{5730}\)
\(2^{-4}=2^\frac{-t}{5730}\)
\(-4=\frac{-t}{5730}\)
\(t=4\cdot5730\)
Analisando os tempos encontrados, o fóssil mais antigo é o 2.
Resposta Questão 11
Alternativa C
Sabemos que o número de infectados se inicia em 2 e triplica a cada semana; seja x o número de semanas, temos que:
\(2\cdot3^x=4374\)
\(3^x=\frac{4374}{2}\)
\(3^x=2187\)
\(3^x=3^7\)
\(x=7\)
Logo, são necessárias 7 semanas.
Resposta Questão 12
Alternativa A
Queremos que:
\(2,5=\frac{80}{2^x}\)
Logo, temos que:
\(2^x=\frac{80}{2,5}\)
\(2^x=32\)
\(2^x=2^5\)
\(x = 5\)
São necessárias 5 meias-vidas para que o césio tenha 2,5 gramas. Como cada meia-vida tem 30 anos, então o total de anos necessários será \(5\cdot30=150\) anos.



