Questão 1
Na figura abaixo, qual é a representação algébrica do número complexo z que, somado a v, tem como resultado u?
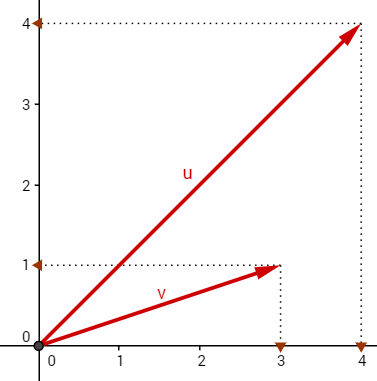
a) z = 1 + 3i
b) z = 3 + 1i
c) z = 4 + 4i
d) z = 3 + 1i
e) z = 1 – 3i
Questão 2
Qual das alternativas abaixo está correta sobre a adição de números complexos?
a) A adição de números complexos pode ser representada geometricamente no plano de Argand-Gauss, mas não a subtração.
b) Ao subtrair dois números complexos, a letra i, referente à raíz quadrada de 1 negativo, sempre desaparece, pois i – i = 0.
c) As somas entre números complexos sempre resultam em um número real e, às vezes, em outro número complexo.
d) Nas somas entre números complexos também valem as propriedades da soma de números reais comutatividade e associatividade.
e) O conjunto dos números reais contém o conjunto dos números complexos.
Questão 3
Seja z = (m2 - 5m + 6) + (m2 – 1)·i, quais seriam os valores de m para que z fosse um imaginário puro?
a) 2 ou 3
b) Apenas 2
c) Apenas 3
d) 0 e 1
e) Apenas 0
Questão 4
Sobre a adição de números complexos, assinale a alternativa correta:
a) A soma de dois números complexos é representada pelo prolongamento de um vetor no plano de Argand-Gauss.
b) A soma de dois números complexos é representada por um vetor, cujas coordenadas são a soma das componentes horizontal e vertical dos vetores que representam os números complexos dados.
c) Se o número complexo z é representado pelo vetor v, então, o produto de z por a (sendo a um número real qualquer) é representado por u, um vetor perpendicular a z.
d) A soma de dois números complexos é representada por uma reta transversal aos vetores que representam esses números complexos.
e) Não é possível representar operações geometricamente.
Resposta Questão 1
É fácil perceber que, se a soma dos complexos “v” e “z” tem “u” como resultado, então, o complexo “z” é obtido pela subtração “u – v”. A representação geométrica dessa operação é a seguinte:
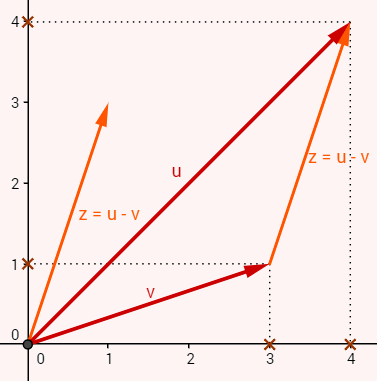
Apenas observando a representação geométrica da subtração u – v, é possível encontrar as coordenadas do vetor “z”, que representa o complexo z e que é a translação do complexo u – v para a origem. Essas coordenadas são: z(1,3) e, portanto, o complexo z = 1 + 3i.
Outra solução pode ser dada da seguinte maneira: os complexos u e v podem ser obtidos sabendo-se que o eixo y representa a parte imaginária do complexo e o eixo x representa a parte real. Logo, u = 4 + 4i e v = 3 + 1i. Daí, segue:
z + v = u
z = u – v
z = 4 + 4i – (3 + 1i)
z = 4 + 4i – 3 – 1i
z = 4 – 3 + 4i – 1i
z = 1 + 3i
Gabarito: Letra A.
Resposta Questão 2
a) Incorreta!
Tanto a adição quanto a subtração de números complexos podem ser representadas no plano de Argand-Gaus.
b) Incorreta!
Ao subtrair dois números complexos, a letra i é tratada como incógnita e, por isso, não desaparece por resultar em zero.
c) Incorreta!
As somas entre números complexos sempre resultam em outro número complexo. Algumas vezes, esse número também é real.
d) Alternativa correta!
e) Incorreta!
O conjunto dos números complexos é que contém o conjunto dos números reais.
Gabarito: Letra D.
Resposta Questão 3
Um número complexo puro é aquele em que a = 0 e b é diferente de zero. Dessa maneira, basta procurar as raízes da equação m2 – 5m + 6 = 0 para encontrar os valores de m para a = 0
m2 – 5m + 6 = 0
a = 1, b = – 5 e c = 6
Δ = b2 – 4ac
Δ = (– 5)2 – 4·1·6
Δ = 25 – 24
Δ = 1
m = – b ± √Δ
2·a
m = – (– 5) ± √1
2·1
m = 5 ± 1
2
m' = 5 + 1
2
m = 6
2
m = 3
m'' = 5 – 1
2
m'' = 4
2
m'' = 2
Para que z seja um número complexo imaginário puro, é necessário que m seja igual a 2 ou 3
Gabarito: Letra A.
Resposta Questão 4
a) Errada!
O prolongamento do vetor é a representação de uma multiplicação por escalar.
b) Correta!
c) Errada!
O produto de v por a é justamente o produto de um vetor por um escalar, cuja representação é o prolongamento do vetor.
d) Errada!
Retas não representam números complexos.
e) Errada!
É possível, sim, representar operações entre números complexos no plano de Argand-Gauss.
Gabarito: Letra B.



