Questão 1
(UFES) A figura a seguir representa dois fios muito longos, paralelos e perpendiculares ao plano da página. Os fios são percorridos por correntes iguais e no mesmo sentido, saindo do plano da página. O vetor campo magnético no ponto P, indicado na figura, é representado por:
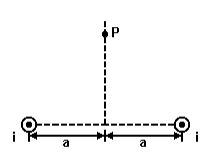
a) ←
b) →
c)↓
d) ↑
e) |B| = 0
Questão 2
(UECE) A figura representa dois fios bastantes longos (1 e 2), perpendiculares ao plano do papel e percorridos por correntes de sentido contrário, i1 e i2, respectivamente.
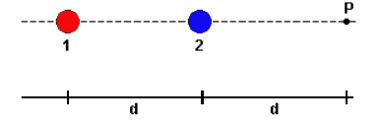
A condição para que o campo magnético resultante, no ponto P, seja zero é:
a) i1 = i2
b)i1 = 2i2
c) i1 = 3i2
d) i1 = 4i2
Questão 3
Duas espiras concêntricas de raios R e 2R conduzem correntes elétricas de sentidos opostos. Sabendo que o campo magnético no centro das espiras é nulo, marque a alternativa que relaciona corretamente o valor das correntes das espiras.
a) A corrente da menor espira deve ser quatro vezes maior.
b) A corrente da maior espira deve ser três vezes menor.
c) A corrente da maior espira deve ser duas vezes maior.
d) A corrente deve ser a mesma nas espiras.
e) A corrente da espira maior deve ser 40% menor.
Questão 4
A figura abaixo mostra duas espiras concêntricas que conduzem correntes elétricas nos sentidos indicados pelas setas. Determine o módulo, a direção e o sentido do campo magnético resultante no ponto O, sabendo que a corrente que passa pela espira maior corresponde ao triplo da corrente que circula a espira menor.
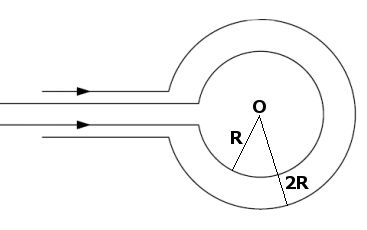
a) O campo em O corresponde à quinta parte do campo da maior espira e sai do plano da página.
b) O campo em O corresponde à metade do campo da maior espira e entra no plano da página.
c) O campo em O corresponde à sexta parte do campo da maior espira e sai do plano da página.
d) O campo em O corresponde à metade do campo da menor espira e entra no plano da página.
e) O campo em O corresponde ao triplo do campo da menor espira e sai do plano da página.
Resposta Questão 1
LETRA “A”
O campo magnético ao redor do fio é circular, e a sua determinação é feita por meio da aplicação da regra da mão direita. Na imagem abaixo, o vetor B representa o campo magnético gerado no ponto p pelo fio da esquerda, e o vetor B' representa o campo magnético gerado pelo fio da direita no mesmo ponto p. A partir da soma vetorial, podemos definir que o campo resultante no ponto p é horizontal para a esquerda.
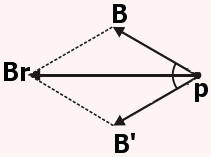
Resposta Questão 2
LETRA “B”
Os campos magnéticos gerados pelos fios no ponto P devem ter o mesmo módulo e sentidos opostos para que o campo resultante seja nulo. Portanto, aplicando a equação do campo magnético para os fios 1 e 2 e igualando essas equações, temos:
BFIO 1 = BFIO 2
μ0 . i1 = μ0 . i2
2 . π . r1 2 . π . r2
i1 = i2
2d d
i1 = i2
2
i1 = 2i2
Resposta Questão 3
LETRA “C”
Para que o campo magnético no centro das espiras seja nulo, as correntes devem circular em sentidos opostos e os campos gerados pelas espiras devem ser iguais. Sabendo que B é o campo magnético, i é a corrente e μ0 é a permissividade magnética, temos:
BESPIRA MENOR = BESPIRA MAIOR
μ0 . iMENOR = μ0 . iMAIOR
2R 2. 2R
iMENOR = iMAIOR
2
2 iMENOR = iMAIOR
Resposta Questão 4
LETRA “D”
A partir da equação que determina o campo magnético para as espiras, encontraremos o campo para cada uma das espiras da figura. Pela regra da mão direita, sabemos que o campo magnético da espira maior (B) entra no plano da página e que o campo da espira menor (B') sai do plano da página.
B' = μ0 . i
2R
B = μ0 . 3i
2 . 2R
B = 3 μ0 . i
2 . 2R
B= 3 B'
2
O campo resultante em O será dado pela subtração de B por B' e terá o sentido de B, já que ele é o maior campo.
BRESULTANTE = B – B'
BRESULTANTE = 3 B' – B'
2
BRESULTANTE =1,5 B' – B'
BRESULTANTE = 0,5 B'
O campo resultante entra no plano da página e vale 0,5 B'.



